5.1. Concepts: Free Fall
Introduction
An object falling freely from a certain height is undergoing free fall motion. If first we assume that air resistance is negligible, the only force acting on the object is the force of gravity, meaning that the object will accelerate towards the surface of the Earth with an acceleration due to gravity: [latex]g = 9.8 \, \text{m/s}^2[/latex].
If air resistance is now taken into consideration, then the object will be subjected to two forces:
- Gravity
- Air resistance
Initially, the force of gravity will be greater than that exerted by air resistance (Figure 5.1 a).
Air resistance increases during the fall (it is directly proportional to the square of the speed), so as the speed of the falling object increases, at some point air resistance might become equal to the force of gravity.
When this happens, the object will continue falling at a constant velocity, called the terminal velocity (Figure 5.1 b).

Concepts
- Throwing an object upwards: the object reaches a maximum height, then comes back to either the same level from which it started or to a different level (for instance, it falls onto another object, it is caught before reaching the initial level on its way back, etc.).
- Throwing an object downwards.
- Dropping an object from a height.
- On its way upward, an object will decelerate with an acceleration equal to [latex]g = 9.8 \, \text{m/s}^2[/latex] (the acceleration due to gravity) until it reaches the maximum height. At the maximum height, the instantaneous velocity is zero.
- On its way downward, an object will accelerate with an acceleration equal to [latex]g = 9.8 \, \text{m/s}^2[/latex] (the acceleration due to gravity).
Example
On the surface of the Moon, the acceleration due to gravity is approximately 6 times less than that on Earth. Throwing an object upwards with velocity [latex]v_i[/latex].
Notations and analysis of the motion
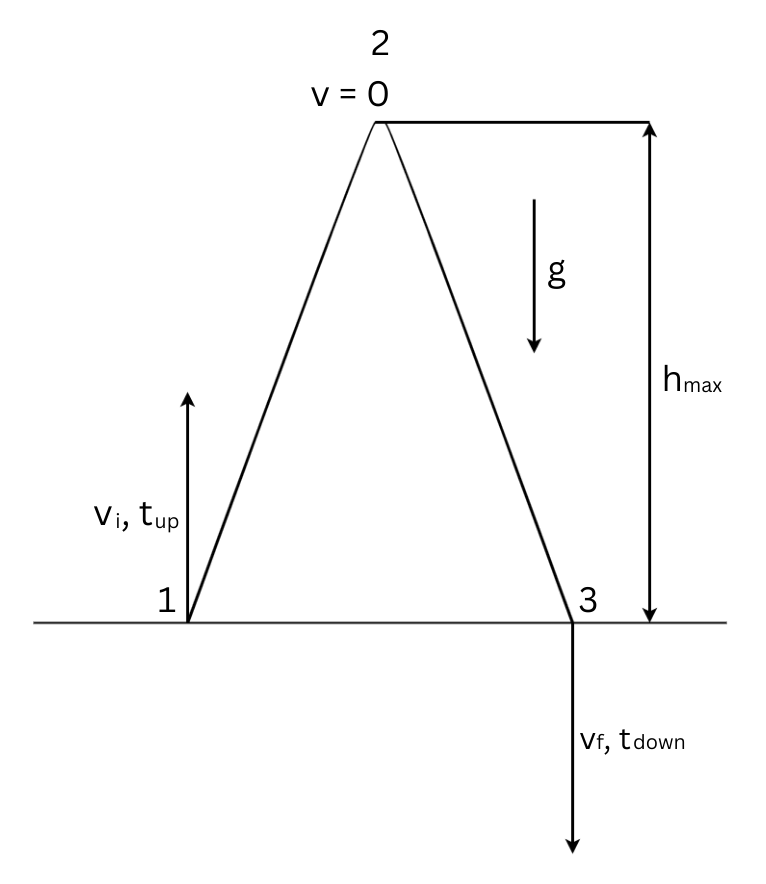
Notations
[latex]v_{i, f}[/latex] - represent the object’s initial velocity and final velocity respectively.
[latex]v[/latex] - represents the velocity at the maximum height (equal to zero).
[latex]h_{max}[/latex] - represents the maximum height reached by the object.
[latex]t_{up, down}[/latex] - represent the time needed to reach the maximum height and the time to come back down from the maximum height respectively.
[latex]g[/latex] - represents acceleration due to gravity.
Analysis of the motion
From point 1 to point 2 (see Figure 5.2):
To calculate the maximum height, we use the following equation:
which becomes:
The acceleration is negative because the object loses speed when going upward (decelerated motion).
From equation (1), the maximum height becomes:
From point 2 to point 3 (see Figure 5.2):
On its way down, the object will come back down from the maximum height, where the velocity is zero, to the same level where it started.
We can express the maximum height using the same formula above:
which becomes:
In this case [latex]v_{i} = 0[/latex], and the acceleration is positive, which means:
Since expressions (2) and (4) represent the same quantity, they are equal.
Conclusion
The initial velocity (at the time of the throw) is equal to final velocity (at the time the object reaches the same level on its way down).
Using this concept, it can be shown that the time to reach the maximum height is equal to the time to come back from the maximum height to the same level.
So, the following equations can be used in solving problems of free fall:
![]() An important note!
An important note!
The equations above are true ONLY for situations in which the object returns to the same level from which it started.
Image Attributions
- Figure 5.1 adapted from:
- A simple sketch of a man sky diving by brgfx courtesy of Freepik

