Chapter equations
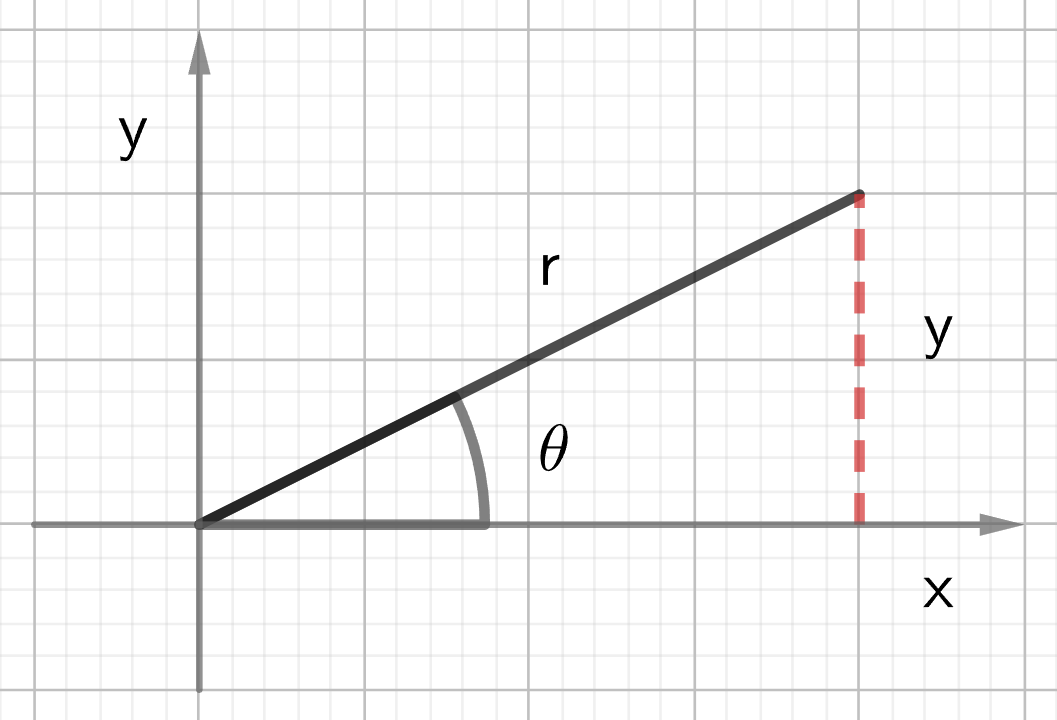
Based on the right-angle triangle in the diagram above:
[latex]x = r \cos \theta[/latex]
[latex]y = r \sin \theta[/latex]
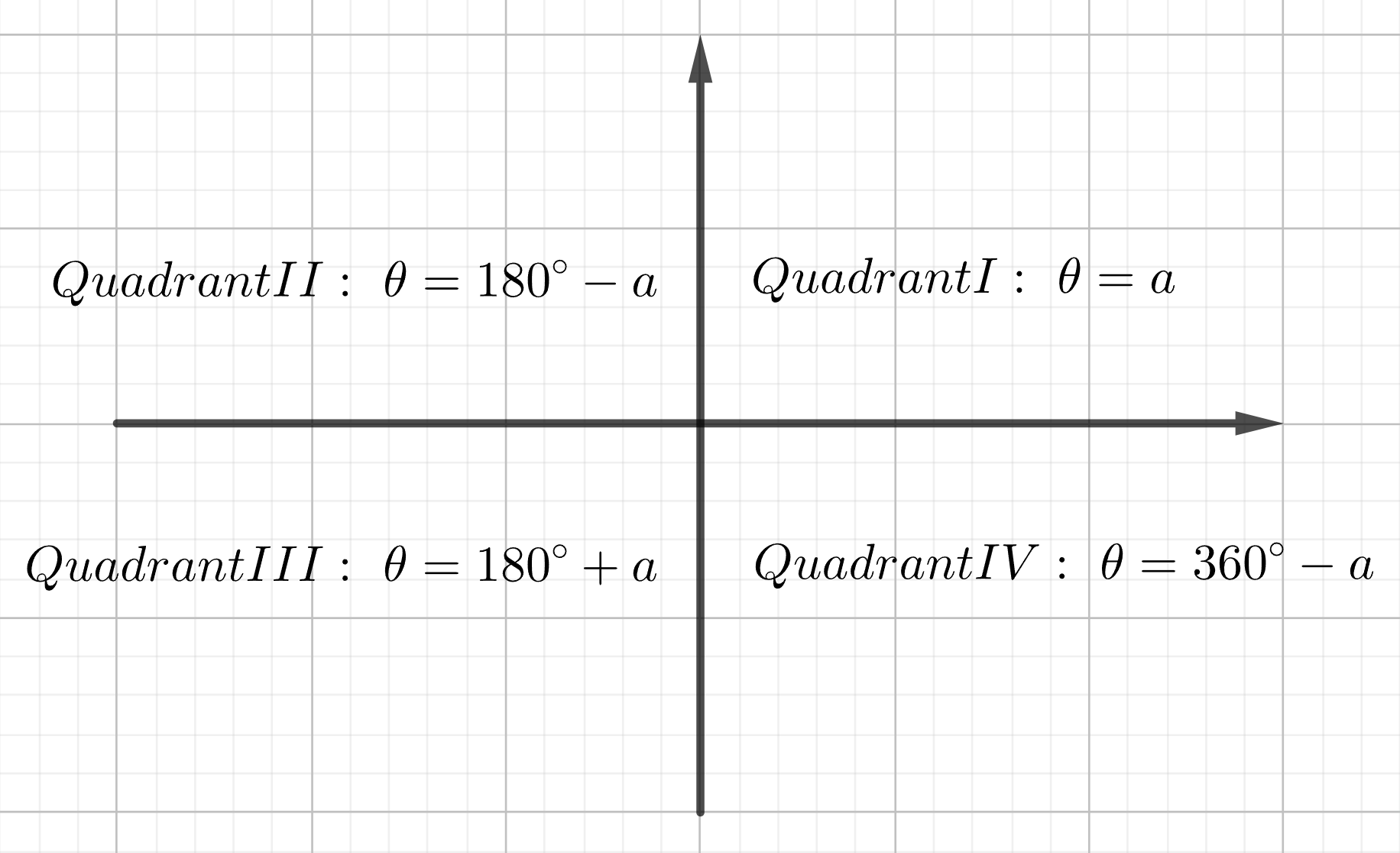
𝛼– the reference angle is, by definition, the shortest angular distance from the terminal side of the angle to the x-axis.
𝜃– the angle in standard position is, by definition, the angle positioned with the vertex in the origin of axes and the initial side on the positive part of the x-axis.
If the Cartesian coordinates are known, the reference angle 𝛼 can be calculated by using the inverse of tangent:
[latex]\alpha = \tan^{-1} \left(\frac{|y|}{|x|}\right)[/latex]
The Pythagorean theorem states that in a right-angle triangle:
[latex]r^2 = x^2 + y^2[/latex]
The relationship between the angle in standard position and the reference angle is:
Try it!
- A vector v is given. The horizontal component of v is vx, while the vertical component of v is vy. Vector v makes an angle with the horizontal of 𝛼. Which equation helps us determine vx?
- A vector v is given. The horizontal component of v is vx, while the vertical component of v is vy. Vector v makes an angle with the horizontal of 𝛼. Which equation helps us determine vy?
- Under which circumstances can we use the Pythagorean theorem to find the resultant of two vectors?
Practice
- Find the x and y components of a force vector F = 35 N, positioned 56° north of west.
Answer:–19.6 N, 29.0 N - Find the x and y components of a velocity vector v = 20 m/s, positioned 25° south of east.
Answer:18.1 m/s, –8.5 m/s - Sketch and find the displacement vector in standard position given the x-component is +32.2 cm and the y-component is –22.2 cm.
Answer:39.1 cm, 325.4° - Sketch and find the displacement vector in standard position given the x-component is –45 cm and the y-component is –75 cm.
Answer:87.5 cm, 239°
Challenge Question
Image Attributions
- Figure 2.4 - 2.5: Created with Geogebra and licensed under CC-BY-NC-SA 3.0.

