Neuron Simulation
Introduction
Neurons are the cells that make up the nervous system. They carry electrical impulses that transmit sensory information, carry signals from the central nervous system to muscles, and many other important functions. The electrical impulses pass between neurons via the synapse, allowing information to be moved to and from the brain from the rest of the body.
In order to process information, neurons must operate at high speeds (i.e. the electric potential on the cell membrane must change very rapidly). The various channels through the membrane transduce external stimuli into changes of the membrane potential. Figure 1 shows a cell membrane and analogous circuit. The cell membrane is a 30-50 ![]() thick layer of lipids, which is analogous to a capacitor in that there is a charge separation across the insulating membrane. Proteins, which act as ionic channels through the membrane, provide a voltage-dependent conduit, which is analogous to a resistor. The battery is analogous to the cell’s resting potential,
thick layer of lipids, which is analogous to a capacitor in that there is a charge separation across the insulating membrane. Proteins, which act as ionic channels through the membrane, provide a voltage-dependent conduit, which is analogous to a resistor. The battery is analogous to the cell’s resting potential, ![]() .
.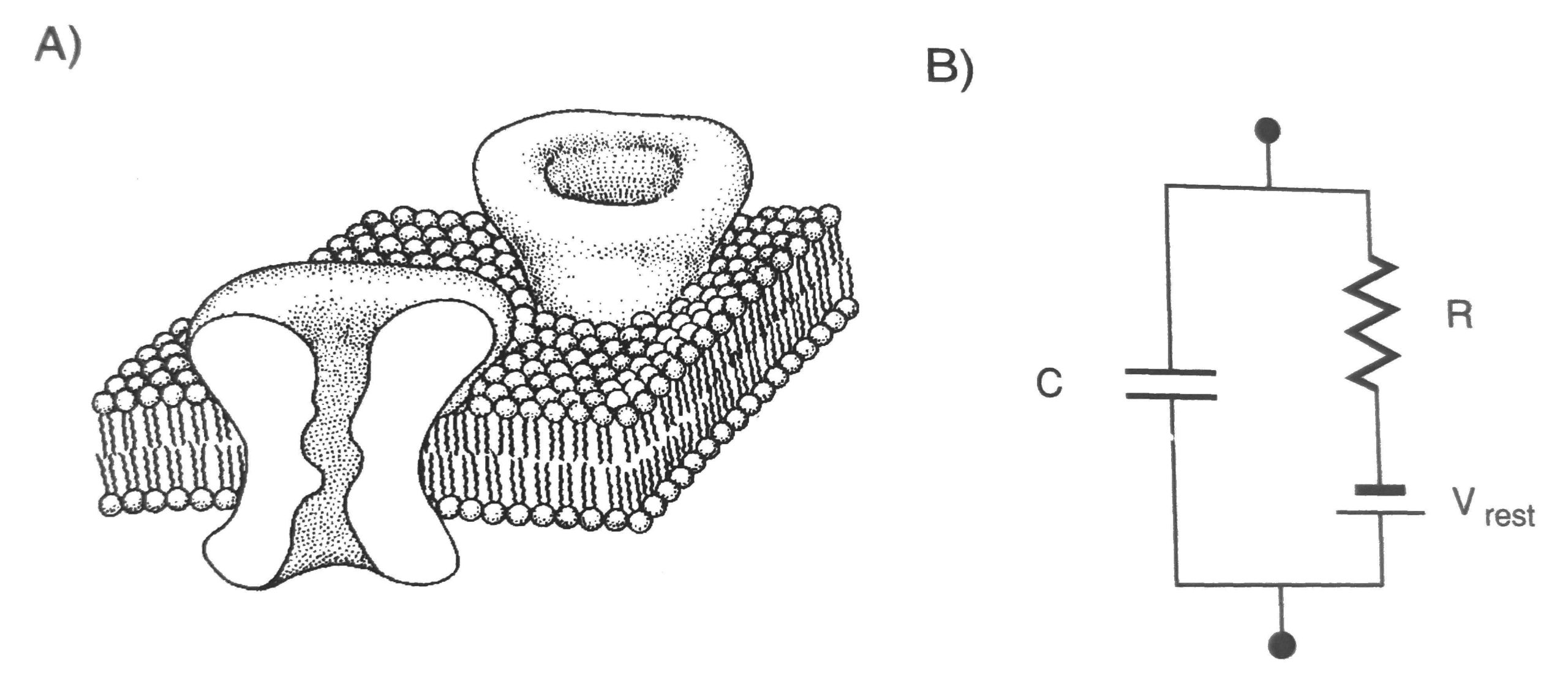 Figure 1: A depiction of a section of cell membrane and its analogous circuit. Figure from reference [1]
Figure 1: A depiction of a section of cell membrane and its analogous circuit. Figure from reference [1]
There are many details regarding how cell membrane capacitance is defined and examples of the values of capacitance, resistance, and potential difference across the membrane in Section 1.1 of the reference text. The main point for our experiment here is that the membrane can be modelled as a capacitance, the proteins through the membrane can be modelled as a resistance, and the firing of a neuron (when the voltage across the membrane is large enough that it will force current through the protein) is modelled by the RC circuit reaching a predefined threshold voltage.
2.1 Integrate-and-Fire
A model of the cell membrane using only a capacitor is the ‘Integrate-and-Fire’ model. The capacitance of the cell membrane integrates charge from the synaptic input until the voltage threshold is reached and the neuron fires. This model captures the charge-integrating nature of the cell membrane, but leaves out several important features. For starters, this model integrates arbitrarily small current injections, so this neuron would fire eventually to even the slightest of external stimuli. Please read the text to find the other glaring flaw in this model. The circuit of the ‘Integrate-and-Fire’ model is shown in Figure 2A.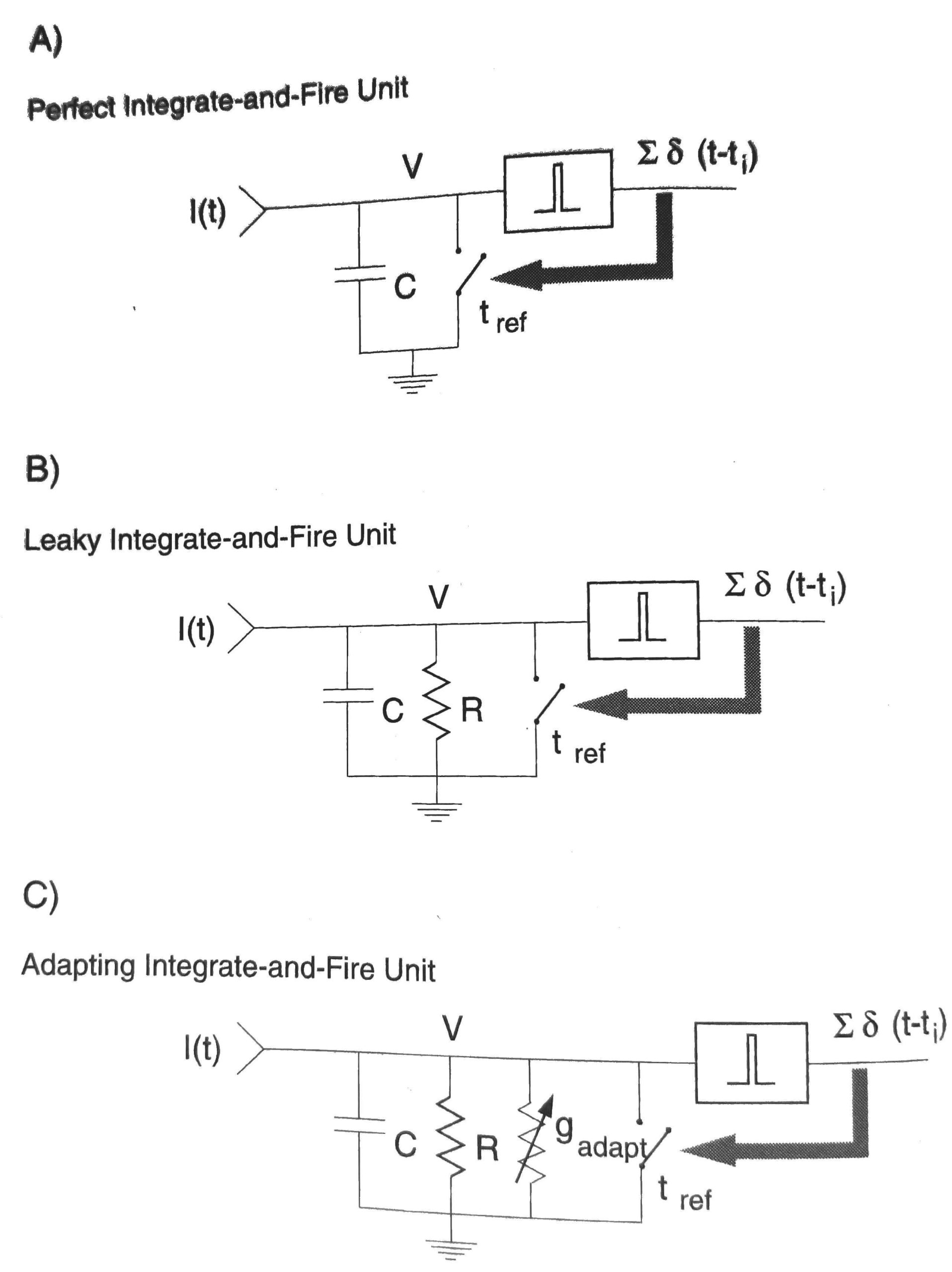
Figure 2: Circuits of the various models this experiment uses to learn about the firing dynamics of neurons. Once the threshold is reached the current injection is shorted to ground for a time ![]() , which simulates the neuron firing and resetting. Figure from reference [1]
, which simulates the neuron firing and resetting. Figure from reference [1]
The equation describing the voltage across the membrane in the Integrate-and-Fire model is really just the definition of capacitance:
(1) ![]()
where ![]() is the charge on the capacitor,
is the charge on the capacitor, ![]() is the capacitance, and
is the capacitance, and ![]() is the voltage difference across the capacitor. Differentiating this equation to determine the time evolution of the voltage gives
is the voltage difference across the capacitor. Differentiating this equation to determine the time evolution of the voltage gives
(2) ![]()
where ![]() is the capacitive current (does current actually flow across the capacitor?). For a given value of
is the capacitive current (does current actually flow across the capacitor?). For a given value of ![]() and
and ![]() , the voltage increases linearly with time until it hits the threshold and the injection current is shunted to ground. Experimental biophysicists characterize a cell’s behaviour by plotting the frequency,
, the voltage increases linearly with time until it hits the threshold and the injection current is shunted to ground. Experimental biophysicists characterize a cell’s behaviour by plotting the frequency, ![]() , of neuronal discharges as a function of injected current:
, of neuronal discharges as a function of injected current:
(3) ![]()
where ![]() is the threshold voltage.
is the threshold voltage.
2.2 Leaky Integrate-and-Fire
The model described in the Introduction that uses a capacitor and resistor is called ‘Leaky Integrate-andFire’, and is shown in Figure 2B. The ‘leakiness’, or ‘forgetfulness’, comes from the resistor, which allows charge to leak out of the capacitor. This model accounts for very small injection currents being truly negligible, and allows the model to simulate the decay of input currents that did not result in the threshold voltage being reached.
The time-evolution of this system is similar to the Integrate-and-Fire equation, with an added term to account for the resistance:
(4) ![]()
It’s left as an exercise to determine that ![]() is given by
is given by
(5) ![]()
where ![]() is the so-called ‘RC’ time constant. The voltage on the membrane increases exponentially until it reaches the threshold voltage
is the so-called ‘RC’ time constant. The voltage on the membrane increases exponentially until it reaches the threshold voltage ![]() , where
, where ![]() is the minimum sustained current capable of inducing
is the minimum sustained current capable of inducing ![]() . Any current above
. Any current above ![]() will result in
will result in ![]() across the cell membrane in time
across the cell membrane in time ![]() :
:
(6) 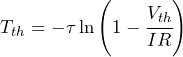
The frequency with which the threshold voltage is reached is
(7) ![]()
What happens when ![]() ? What happens when
? What happens when ![]() ?
?
2.3 Adapting Leaky Integrate-and-Fire
One last variant in the model that proves very useful is adding an adapting conductance to the circuit, as shown in Figure 2C. The conductance starts out at zero (i.e. infinite resistance, thereby not changing the circuit from the Leaky Integrate-and-Fire model) and increases each time the ‘neuron’ fires. As the conductance increases, more and more current is shunted to ground instead of charging the capacitor. The result is that it takes longer and longer to reach the threshold voltage required for the ‘neuron’ to fire. The conductance decreases (i.e. returns to zero) exponentially between neuron firings. This model captures the adaptability of our senses to ignore constantly-present stimulus like mild odors or discomfort, while resetting if the stimulus is removed.
The adapting conductance changes Equation (4) ever so slightly:
(8) ![]()
where ![]() is the value of the adapting conductance.
is the value of the adapting conductance.
