Procedure

Initial Angular Momentum

Be VERY careful as you use these magnets. DO NOT let them close to each other if your fingers are also close by. I don’t know if you’ve ever dropped a 10-pound weight on the tip of your finger, but that’s what it will feel like.

You should only ever be pulling the magnets apart after the collision. As long as you don’t bring them near each other while they are in your hands, you should be fine.

1. Start by taking the measurements you will need in order to determine the initial angular momentum .
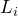2. Use a ruler to measure about 10 cm up each inclined ramp.
3. Use a protractor to measure the angle of the incline. Assume it’s the same for both ramps.
4. Use the caliper to confirm that the distance between the grooves of the ramp are indeed 1⁄4”. The caliper are metal and can scratch the acetal, so be gentle.
5. Use these measurements to determine the velocity the magnets will reach at the bottom of the incline due to their initial potential energy as in Equations (5) in the Introduction section and Equation (1) in the Apparatus section. Do the two equations result in very different velocities?
6. We’ll assume that the magnets don’t lose much energy as they roll down the ramp and that the calculated velocity is the actual velocity.
7. When using two magnets from a set height, the distance between the rivets sets the initial value of angular momentum (L_i). Start out with rivets that are 1⁄2” apart and calculate L_i.

Determining

1. Plug the pickup coil into channel 1 of the oscilloscope.
2. On the oscilloscope, open the trigger menu. You want to be triggering from channel 1, and for the trigger level to be 50-100 mV. Set the time of the trigger to be at least a few hundred milliseconds from the left of the scope display.
3. Set the vertical and horizontal scales for a signal up to 1 V in amplitude and anywhere from 100 ms to 10 s long.
4. Hold the two 3⁄8” magnets at their height markers. Use tracks that are 1⁄2” apart. Let them go!
5. The oscilloscope should have triggered and you should see something that looks like the signal in Figure 3, but note that the length of the decay of the oscillations after impact varies greatly from run to run. Sometimes the magnets revolve for tens of seconds, and sometimes less than a few revolutions.
6. You will need to zoom in on the first few rotations after impact and determine the rotational frequency of the magnets. You may need to do another run with a shorter timescale on the oscilloscope in order to zoom in enough.
7. Use the cursors to determine the wavelength of your signal, NOT the wavelength from the measurement menu. You have your first data point!
8. You can control the value b and v to vary the initial value of angular momentum L_i. Vary this value as much as you can while still generating a rotating dumbbell. Take as many data points as you need.
9. Collect another set of data with the 1⁄2” magnets. Does the strength of the magnetic field change your measured value of the rotational inertia of the system? How does the oscilloscope signal change compared to when you were using the smaller magnets.

Analogy to Gravitational Waves

1. Hold the two 3⁄8” magnets at their height markers. Use tracks that are 1⁄2” apart. Let them go!
2. Your magnets should rotate quite rapidly near the center of the baseplate for quite a while. On occasion, the rotation stops quite rapidly due to the magnets aligning their poles AFTER contact.  That’s the scenario you want to measure here.
3. In either case, collect an oscilloscope trace that shows the inward spiral, merger, and ringdown as if this were an experiment that observed the merger of two black holes. Save this scope trace on a USB stick in order to send yourself the data.