Introduction

2.1 The Michaelson Interferometer

The term `interferometry’ is used to describe a huge variety of experiments that use the constructive and destructive interference of waves to detect some change or make some measurement. I am trying to keep lab manuals to less than 7 pages, so I can’t list all of the applications in all of the various fields of research where interferometry is useful. Feel free to spend some time browsing Wikipedia if you’re interested. In this experiment, the wave you will use is an electromagnetic wave from a diode or helium-neon laser. The light enters a Michelson interferometer is shown schematically in Figure 1.

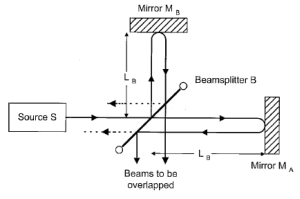
A beam-splitter creates two beams from the input to the interferometer. Two mirrors are set the same distance from the beam splitter. The input beam is aligned such that the beam paths in each arm of the interferometer are perfectly overlapped, allowing the user to detect the constructive and destructive interference of the beams. In the electromagnetic wave from one of the lasers, this interference will present itself as bright and dark fringes in the output beam.

Interferometers are exclusively used to measure changes. An interferometer that has two static arms is not all that useful. Phenomenon like gravitational waves can be detected because they affect one arm and not the other. Let’s say that we change the length of one arm of the interferometer by some distance . If we monitor the output beam as the interferometer is changed, we should see it go from very bright (constructive interference) to very dark (destructive interference) and back to very bright every time the length of the arm is increased by one wavelength of the laser. This information is contained in the following equation

where is the distance that one of the mirrors has moved, is the wavelength of the laser, and is the number of wavelengths that have been moved through. The factor of 2 comes from the fact that the light must travel from the beam-splitter, to the mirror, and back again, meaning that it travels twice the distance moved by one of the mirrors.

2.2 Thermal Expansion

It should come as no surprise that most materials expand when heated.  The atoms and molecules in the material vibrate more vigorously as the temperature increases, leading to expansion.  The length expanded by a column of material under heat depends on the original length of the material.  The thermal coefficient, , is given by

$\alpha = \frac{1}{L}\frac{\Delta L}{\Delta T},

which is expressed as a length per unit length, usually ppm/K.  Longer materials expand further because there is more material to expand.  This point is very important in the engineering of large structure like bridges and buildings, but is non negligible on smaller scales if high precision is important.