Introduction

The photoelectric effect is the observed phenomenon of electrons being ejected from the surface of a material (almost exclusively metals) when it is exposed to light of a sufficiently high energy. Classically, the photoelectric effect would be attributed to the transfer of energy from incoming light to an electron. If that were true, then the rate at which electrons are ejected from a metal sample would depend on the intensity of the incoming light. And for a sufficiently low intensity, there would be a delay between when the light is applied, and when the first electron gains enough energy to be ejected. As you will demonstrate, this theory is at odds with the experimental results, which means that it’s time for a new theory.

    The work of many physicists such as Einstein, Hertz, Millikan, and others, eventually lead to the concept of quantized light: That light is not a wave, but actually many small, discrete wave packets, which we now call photons, with energy:

(1)  

where  is the frequency of the light packet, and  is Planck’s constant.

    The electrons are bound inside the metal surface with energy where is the elementary charge and  is the ‘work function’. The photoelectric effect is actually how the work function is defined: It’s the energy needed to remove an electron from a solid. Therefore, if

(2)  

    then an electron will never be ejected from the surface of the metal, regardless of intensity of the light. If

(3)  

    then electrons will be ejected, and the excess energy appears as kinetic energy. It’s the kinetic energy of the electron that we’re going to use to probe the photoelectric effect. Consider an apparatus like the one shown schematically in Figure 1. We’ll apply a potential bias to the anode. This retarding potential will stop electrons from leaving the surface of the cathode unless they have kinetic energy greater than . Putting all this together, we have the following equation for the energy of the photoelectron:

(4)  

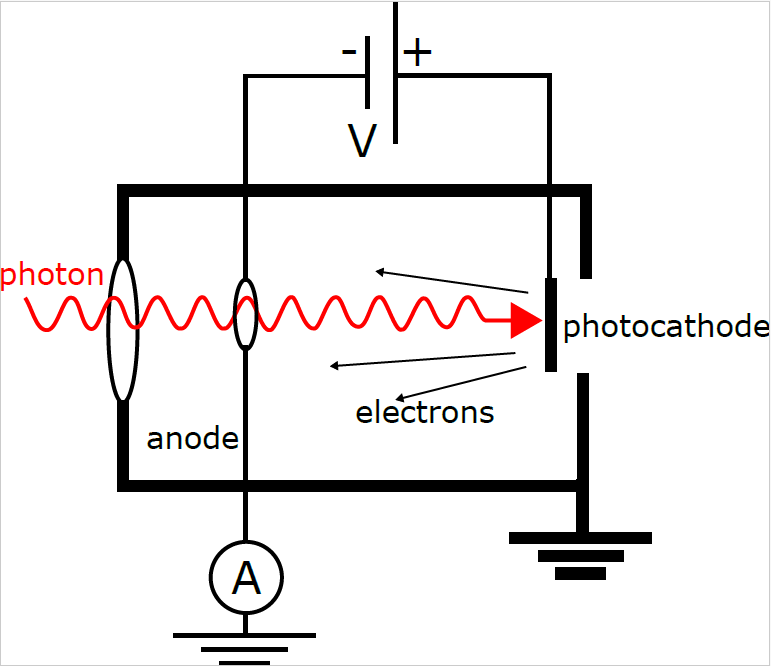
Figure 1: A schematic representation of the photoelectric effect apparatus. Photons pass through a hole
in the anode and hit the photocathode. The photoelectrons generate a current that can be measured
with an ammeter (or electrometer). The anode can be biased relative to the photocathode to retard the
photoelectrons, thereby probing their kinetic energy.

    If one can determine the maximum value of the retarding potential at which the photoelectrons can still overcome it, and one knows the frequency of light that generated the photoelectrons, then one can generate a set of data with a linear trend, the slope of which gives . This technique of measuring the kinetic energy of charged particles using a retarding potential is a super common [?].