Introduction

Daniel FitzGreen

Neuron Simulation

Introduction

Neurons are the cells that make up the nervous system. They carry electrical impulses that transmit sensory information, carry signals from the central nervous system to muscles, and many other important functions. The electrical impulses pass between neurons via the synapse, allowing information to be moved to and from the brain and the rest of the body.

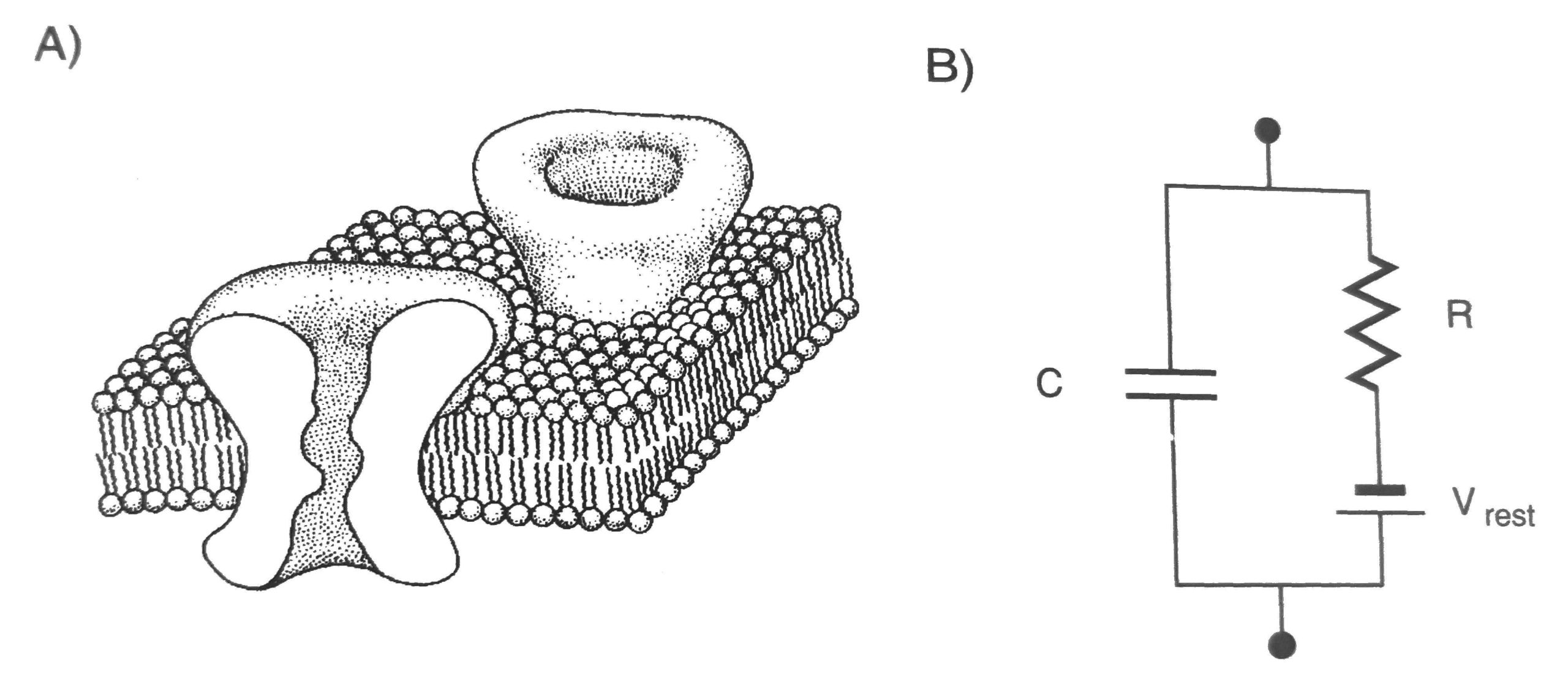
In order to process information, neurons must operate at high speeds (i.e. the electric potential on the cell membrane must change very rapidly). The various channels through the membrane transduce external stimuli into changes of the membrane potential. Figure 1 shows a cell membrane and analogous circuit. The cell membrane is a 30-50 $\mathrm{\AA}$ thick layer of lipids, which is analogous to a capacitor in that there is a charge separation across the insulating membrane. Proteins, which act as ionic channels through the membrane, provide a voltage-dependent conduit, which is analogous to a resistor. The battery is analogous to the cell’s resting potential, $V_{\text{rest}}$ .

There are many details regarding how cell membrane capacitance is defined and examples of the values of capacitance, resistance, and potential difference across the membrane in Section 1.1 of the reference text. The main point for our experiment here is that the membrane can be modelled as a capacitance, the proteins through the membrane can be modelled as a resistor, and the firing of a neuron (when the voltage across the membrane is large enough that it will force current through the protein) is modelled by the RC circuit reaching a predefined threshold voltage.

3.1 Integrate-and-Fire

A model of the cell membrane using only a capacitor is the ‘Integrate-and-Fire’ model. The capacitance of the cell membrane integrates charge from the synaptic input until the voltage threshold is reached and the neuron fires. This model captures the charge-integrating nature of the cell membrane, but leaves out several

Figure 1: A depiction of a section of cell membrane and its analogous circuit. Figure from reference [1]

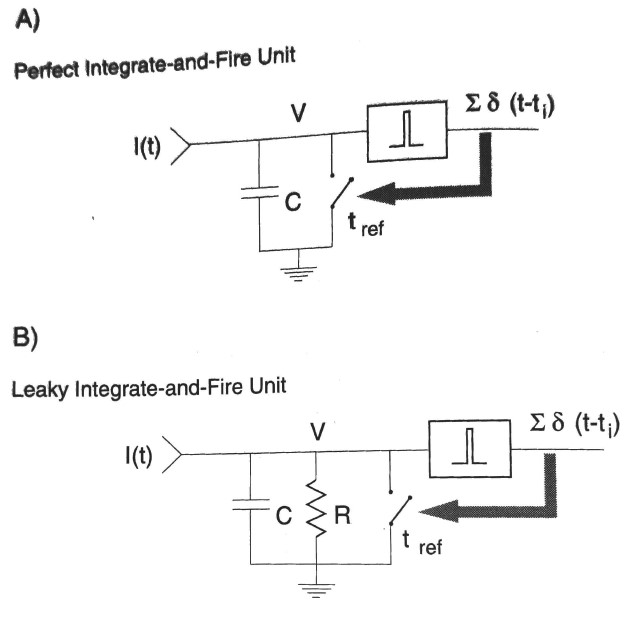
important features. For starters, this model integrates arbitrarily small current injections, so this neuron would eventually fire from even the slightest of external stimuli. The circuit of the ‘Integrate-and-Fire’ model is shown in Figure 2A.

The equation describing the voltage across the membrane in the Integrate-and-Fire model is really just the definition of capacitance:

(1) $\begin{equation*} Q = CV, \end{equation*}$

where $Q$ is the charge on the capacitor, $C$ is the capacitance, and $V$ is the voltage difference across the capacitor. Differentiating this equation to determine the time evolution of the voltage gives

(2) $\begin{equation*} I = C \cfrac{dV(t)}{dt},\end{equation*}$

where $I$ is the capacitive current (does current actually flow across the capacitor?). For a given value of $I$ and $C$ , the voltage increases linearly with time until it hits the threshold and the injection current is shorted to ground. Experimental biophysicists characterize a cell’s behaviour by plotting the frequency, $f$ , of neuronal discharges as a function of injected current:

(3) $\begin{equation*} f = \cfrac{I}{CV_{th}},\end{equation*}$

where $V_{th}$ is the threshold voltage.

3.2 Leaky Integrate-and-Fire

The model described in the Introduction that uses a capacitor and resistor is called ‘Leaky Integrate-and-Fire’, and is shown in Figure 2B. The ‘leakiness’, or ‘forgetfulness’, comes from the resistor, which allows charge to leak out of the capacitor. This model accounts for very small injection currents being truly negligible, and allows the model to simulate the decay of input currents that did not result in the threshold voltage being reached.

Figure 2: Circuits of the various models this experiment uses to learn about the firing dynamics of neurons. Once the threshold is reached the current injection is shorted to ground for a time tref, which simulates the neuron firing and resetting. Figure from reference [1]

The time-evolution of this system is similar to the Integrate-and-Fire equation, with an added term to account for the resistance:

(4) $\begin{equation*} C\cfrac{dV(t)}{dT} + \cfrac{V(t)}{R} = I(t).\end{equation*}$

$V(t)$ is given by

(5) $\begin{equation*} V(t) = IR(1-e^{-t/\tau})+V_{(t=0)}e^{-t/\tau},\end{equation*}$

where $\tau = RC$ is the so-called ‘RC’ time constant. The voltage on the membrane increases exponentially until it reaches the threshold voltage $V_{th} = I_{th}R$ , where $I_{th}$ is the minimum sustained current capable of inducing $V_{th}$ . Any current above $I_{th}$ will result in $V_{th}$ across the cell membrane in time $T_{th}$ :

(6) $\begin{equation*} T_{th} = -\tau \ln(1-\cfrac{V_{th}}{IR}).\end{equation*}$

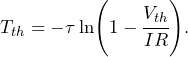
The frequency with which the threshold voltage is reached is

(7) $\begin{equation*} f = \cfrac{1}{T_{th}+t_{\text{ref}}}=\cfrac{1}{t_{\text{ref}}-\tau\ln(1-V_{th}/IR)}\end{equation*}$

Introduction

3.1 Integrate-and-Fire

3.2 Leaky Integrate-and-Fire

License

Share This Book