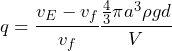Introduction

Daniel FitzGreen

Milikan Oil Drop

Introduction

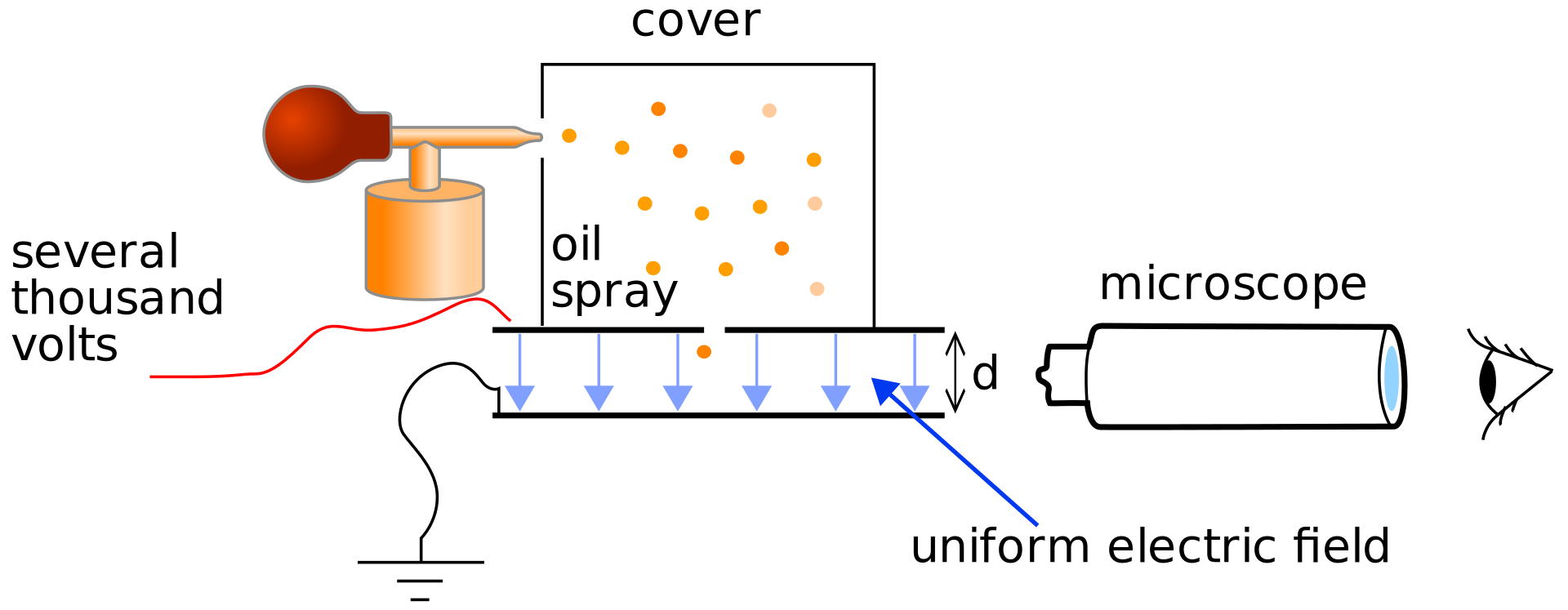
Millikan is credited with proving the discrete nature of electric charge and, at the time, the most precise measurement of the electric charge (maybe credited too much [2]). His experiment (shown schematically in Figure 1), used oil droplets that picked up a small number of charges as they entered the experiment chamber. And if that didn’t work, he blasted them with X-rays to ionize some gas, thus providing free negatively-charged electrons and positively-charged ions.

Figure 1: A schematic representation of Millikan’s original oil drop experiment. Figure from Wikipedia

The velocity of the charged oil droplets was measured with and without an applied electric field. By monitoring only the slowest droplets, and taking many precise measurements, Millikan was able to see that the charge on the oil droplets came in integer values of what we now know to be the elementary charge.

Without an electric field, the gravitational force on an oil droplet is equal to the drag force that the droplet experiences as it moves through a viscous fluid (i.e. air):

(1) $\begin{equation*} mg - kv_f =0,\end{equation*}$

where $m$ is the mass of the droplet, $g$ is the gravitational constant, $v_f$ is the free-fall velocity of the droplet, and $k$ is some constant relating the terminal velocity to the viscous force. The small spheres very quickly reach terminal velocity, so we can ignore the very short time in which they are accelerating.

We add an extra term to the above equation when we apply an electric field:

(2) $\begin{equation*} mg - kv_E + Eq = 0,\end{equation*}$

where $v_E$ is the droplet’s velocity in the electric field, $E$ is the magnitude of the applied electric field, and $q$ is the electric charge of the droplet. The value of $k$ is the same in each equation, and rather difficult to calculate. We’ll make life easier on ourselves by solving both of the above equations for $k$ and setting them equal to each other. Then we have the following equation for the electric charge of the droplet:

(3) $\begin{equation*} q = \cfrac{v_E-v_f}{v_f}\cfrac{mg}{E}.\end{equation*}$

Seems pretty simple so far, but the devil is in the details. Millikan used oil droplets that varied in size and mass, and so he had to take a bunch of measurements of the droplets free-fall velocity in order to solve for its radius. Then, using the density of the oil, $\rho$ , he could solve for the mass. The electric field is far easier to deal with since it is generated by a parallel plate capacitor, where $E=V/d$ , with $V$ being the applied voltage and $d$ is the distance between the plates.

Putting this all together, we can solve for the charge on an oil drop if we can measure its radius and velocity in a known electric field.

(4) $\begin{equation*} q = \cfrac{v_E-v_f}{v_f}\cfrac{\frac{4}{3}\pi a^3\rho gd}{V}\end{equation*}$

Introduction

License

Share This Book