4.1 Software

A webcam is used to take pictures of the lensed image. A Python script runs on the PC and allows students to save the current frame from the webcam as an image file. To save images, click on the image of the webcam live feed and press ‘q’. You may have to hold it down for a second. The Python output should read ‘frame saved’ and your image file should be saved to the desktop. If you want to stop the program, hold ‘Esc’.

4.2 Alignment

1. Mount the camera and the 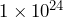 kg point-mass lens in their holders (if they’re not there already). The thickest of point-mass lenses need to be held in the large, claw-like holder since they don’t fit in the small black lens holders.
2. Slide the lens so that it is relatively close to the camera and adjust the position of the lens and camera so that the lens is well-centered with the camera’s field of view. Now slide the lens so that it is far away from the camera, and adjust the camera angle so that the lens is well-centered with the camera. You may need to do a few iterations of these steps to get the camera and lens well aligned. The alignment doesn’t have to be perfect.
3. Slide the lens to about halfway between the camera and the black backdrop. Tape the image of the blue dot on the backdrop so that you see a nice, full Einstein ring. Slide the lens closer and further away from the camera and make sure you still mostly see the Einstein ring as the lens is moved. If the ring turns into one or two arcs or dots, then you may have to make small adjustments in the alignment as you carry out the experiment.

4.3 Strong Gravitational Lensing as a Function of Distance

1. Start with the 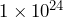 kg point-mass lens. Use the Python program to save an image of the whole lens (you need the lens itself as a distance calibration). Determine the diameter of the Einstein ring and lens in units of pixels. Use the known diameter of the lens to determine the diameter of the Einstein ring in units of meters. Do NOT confuse this diameter for half of the Einstein radius 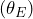, which is actually an angle.
2. Calculate  from your position measurements.
3. From all of these measurements, you should be able to calculate the emulated mass of the lens and its uncertainty. Set up a spreadsheet so that you can quickly determine the emulated mass from your measurements.
4. Scan as large a range of the distance variable as you can AND have at least 5 values. If your mass measurements aren’t consistent, STOP! You are doing something wrong; probably just the calculations. Keep in mind that the angle involved are ‘small’.

4.4 Strong Gravitational Lensing as a Function of Mass

1. Now switch to the thinner lenses that fit into the black lens holders. The mass of each lens is etched on the side.
2. Place the lens somewhere near the middle of the observer and the source image. Use the same steps as above to determine the emulated mass of the lens. You only need a single measurement.
3. Swap the lens and take measurements until the lens is too weak to generate an Einstein ring (you may have to move the observer and lens to see the ring). You should finish with a data set of expected masses and measured masses.