Rotational Inertia
Introduction
Conservation of Angular Momentum
Conservations laws are incredibly useful rules in physics. If the total energy or momentum of a system is known, then physicists can often infer where lost energy or momentum in a system has gone and hopefully learn something interesting. Consider a system of two bodies as shown in Figure 1. The bodies (spheres) are moving on parallel trajectories, each with some velocity v, separated by some distance b called the impact parameter. The total angular momentum of such a system is
(1) ![]()
Since we are imagining this whole scenario anyway, we can just say that m1 = m2 = m and v1 = v2 = v.
Then the initial angular momentum is
(2) ![]()
If the two bodies experience a mutually attractive force (i.e. magnetic, gravitational) then the bodies will collide and rotate to conserve angular momentum. The angular momentum of such a system is
(3) ![]()
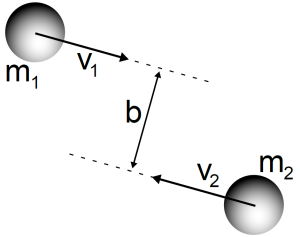
Figure 1: Two mutually-attracted bodies with linear trajectories offset by a distance b called the impact parameter.
where r is the radius of the sphere, ![]() is the rotational inertia of the two-sphere system (which looks like a dumbbell) and ωf is the angular frequency of the spinning dumbbell. If angular momentum is conserved, then Li = Lf and the angular momentum of two attracted bodies a great distance apart is equal to the angular momentum of the rotating system after it has merged.
is the rotational inertia of the two-sphere system (which looks like a dumbbell) and ωf is the angular frequency of the spinning dumbbell. If angular momentum is conserved, then Li = Lf and the angular momentum of two attracted bodies a great distance apart is equal to the angular momentum of the rotating system after it has merged.
Rotating Spherical Magnets
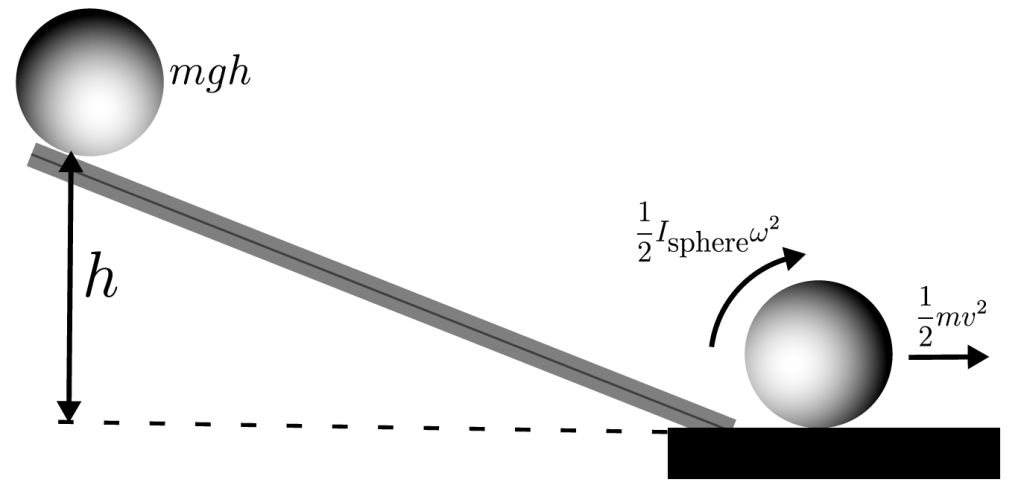
Figure 2: The dynamics of rolling a sphere down an incline plane. It is assumed that the sphere rolls without slipping.
In this experiment specifically, the bodies are magnetic spheres. The velocity of the spheres is gained via acceleration down an inclined plane. If the spheres are at some height h, then their potential energy is ![]() . As the sphere rolls down the incline plane, the potential energy will convert into kinetic energy in the form of the translational velocity and rolling motion of the sphere, as shown in Figure 2. The kinetic energy is
. As the sphere rolls down the incline plane, the potential energy will convert into kinetic energy in the form of the translational velocity and rolling motion of the sphere, as shown in Figure 2. The kinetic energy is
(4) ![]()
where ![]() is the rotational inertia of the sphere
is the rotational inertia of the sphere ![]() and ωi is the angular frequency of the rotation of the single sphere. Assuming the sphere does not slip as it rolls, then v = ωir and the kinetic energy simplifies to
and ωi is the angular frequency of the rotation of the single sphere. Assuming the sphere does not slip as it rolls, then v = ωir and the kinetic energy simplifies to
(5) ![]()
Equating the potential and kinetic energies (since energy is conserved) results in the velocity of the spheres after acceleration:
(6) ![]()
If the impact parameter b is known, then the initial angular momentum can be calculated from Equation (2). The final angular momentum (Equation (3)) can be calculated if the rotational frequency of the post-collision spheres can be measured. One way to confirm the conservation of angular momentum is to use the measured rotational frequency to experimentally determine its rotational inertia and compare it to the accepted value.
Electromagnetic Radiation
The magnetic spheres rotate and eventually come to a stop due to energy-loss via friction. But even in an ideal, frictionless world, the spheres would eventually come to a stop because they are constantly losing energy by radiating an electromagnetic field. One can detect the short-range, quickly changing magnetic flux using a short solenoid, whereby a voltage is generated via electromagnetic induction. The more turns the coil has, the larger the voltage due to the changing magnetic field will be according to
(7) ![]()
where N is the number of turns in the coil and φ is the magnetic flux.
Analogy to Colliding Blackholes
The collision and rotation of the magnetic spheres is analogous to how black holes collide and rotate. The physics obviously isn’t too similar since (among other reasons) the black holes merge into a single body and the magnets don’t, but the measured signal from the rotating magnets shows the characteristic inward spiral, merger, and ringdown seen in the signal from merging black holes, an example of which is shown in Figure 3.
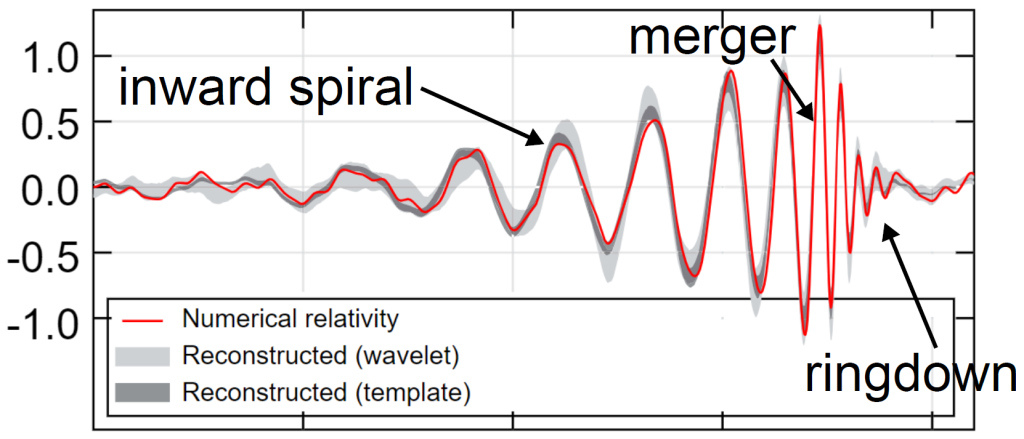
the characteristic inward spiral, merger, and ringdown.
