4.1 Inductors as Filters

1. Build the circuit shown in Figure 5(a) with a 200 Ohm resistor.
2. Use a square wave from the PASCO interface at 1000 Hz.
3. Use the oscilloscope to measure the voltage across the inductor. You should see a familiar sight: A square wave with the DC/low-frequency part of the signal filtered out.
4. Use the same technique as Lab 3 to measure the time constant (the time between one point on the curve and of that value). Use that measured time constant to estimate the inductance you are using.
5. Swap the position of the resistor and inductor (as shown in Figure 5(b)) and set up the oscilloscope to measure across the resistor. Start without any resistor present (the oscilloscope has a MASSIVE internal resistance). The resistor adds a damping effect to the oscillations. Zoom in on the ‘corner’ of one of the square waves.  Think about what you’re seeing.
6. Insert the 22 k 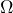resistor, then the 2.2 k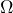, then 200 Ohm resistors and comment on how the filter behaviour changes. Are you seeing underdamped, overdamped behaviour? It may be critically damped but it’s unlikely that we have exactly the right component values for that. Don’t worry about quantifying the damping; we’re just observing and thinking here.
7. With the 200 Ohm resistor in place, change the frequency until you find the cut-off frequency for this low-pass filter.
8. Just for fun, set the frequency to 1 Hz and hold the compass near the hole through the inductor. What do you notice?

Figure 5:  (a) high pass filter using an inductor and resistor, (b) low pass filter.

4.2 RLC Bandpass Filter

1. Build the circuit shown in Figure 2. Set the oscilloscope to measure across the resistor.
2. Set the PASCO universal controller to output a sine wave.  Vary the frequency from the PASCO controller to find the resonant frequency. Take about 5 amplitude measurements on either side of the resonant frequency. Make sure you measure the upper and lower cut-off frequencies.
3. Check that your measured resonant frequency matches your calculation from Equation (2).
4. Calculate the  of your circuit from Equation (3).