Introduction

nejatsm

10 Introduction

The goal of this lab is to measure the restoring force, stored energy, and oscillation period of a spring.

An elastic spring is described by Hooke’s Law, which states that the force $F$ required to stretch or compress the spring by a distance $x$ from its unstretched length is proportional to $x$ . This is expressed as

(1) $\begin{equation*} F = k\Delta x \end{equation*}$

where $F$ is the applied force, $x$ is the displacement of the spring from its unstretched length and $k$ is the stiffness constant of the spring, also called the spring constant. The restoring force exerted by the spring is equal and opposite to the applied force.

If a spring obeys Hooke’s Law, the work required to stretch or compress the spring from an initial displacement $x_0$ to a final displacement $x$ is:

(2) $\begin{equation*} W = \frac{1}{2}kx^2-\frac{1}{2}kx_0^2 \end{equation*}$

Thus, if the spring is initially unstretched so that $x_0=0$ ,

(3) $\begin{equation*} W = \frac{1}{2}kx^2 \end{equation*}$

The work that is done is stored as potential energy in the spring. In this experiment, one end of the spring is fixed and x is measured as the change in position of the other end from its position when the spring is not stretched.

If a mass is attached to a spring obeying Hooke’s Law and set into oscillation, the motion is called simple harmonic motion (SHM). The frequency of the motion is

(4) $\begin{equation*} f = \frac{1}{2\pi}(\frac{k}{m_t})^\frac{1}{2} \end{equation*}$

where $m_t$ is the total mass involved in the oscillation. The period is independent of the amplitude of the oscillation. From Equation (4), $1/f^2$ is proportional to $m_t$ . This relationship will be tested in this experiment. In order to obtain the frequency $f$ , we will measure the period of oscillation $T$ , and use the relation $f=1/T$ .

Figure 1: Set-up for measuring spring constant

APPARATUS

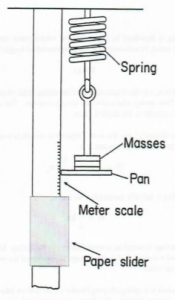
The spring is hung from a support clamp. A pan whose mass is 50g is attached by a hook to the bottom of the spring. Slotted 20 gm (gm are the units shown on the masses) and 50 gm masses are placed on the pan as required. The position of the bottom edge of the pan is measured with a one-meter ruler. In all of your measurements, the zero end of the meter ruler will be placed at the top so that the ruler reading increases as the spring length increases. A change in length of the spring is reflected in a similar change in position of the pan. Make a paper slider by taking a small piece of paper, fold it around the ruler. Tape its two ends together, allowing it to move up and down freely when hit by the bottom of the pan. The paper slider is used in part 2 of the measurements to record the lowest position of the moving pan.

MEASUREMENTS

All work in this experiment should include a proper treatment of the uncertainties involved.

IMPORTANT!!! Do not hang more than 250 grams of mass from the spring, or stretch the springs beyond an equivalent amount as they can become permanently deformed (which ruins the springs and invalidates your results). Once you are done making your measurements, please remove the pan and the weights from the spring. Leaving them on for a long time can also permanently deform the spring. Mass values are accurate to 1%.

10 Introduction

APPARATUS

MEASUREMENTS

License

Share This Book