Lab 9: Simple Harmonic Motion
Lab 9: Simple Harmonic Motion
Exercise 1
a) What does it mean for a force to be “linear in displacement”?
b) Is the gravitational force (near the Earth’s surface) linear in displacement? How would you conduct an experiment that would prove that it is or not?
Why are we interested in linear forces? Because over a short enough range, any function looks linear! For this reason, the physical system with a restoring force directly proportional to the displacement, should be fairly common. Let us consider the implications for the motion of the object acted on by such a linear force.
If the net force acting on the object is a restoring force that in linear in displacement, i.e.
[latex]F_{NET} = -cx[/latex]
then according to Newton’s second law:
[latex]ma = -cx[/latex]
But [latex]a[/latex], the acceleration of the object, and [latex]x[/latex], the position of the object, are not independent variables. As you know, the acceleration is the second time derivative of the position function i.e.
[latex]m\frac{d^2x}{dt^2}=-cx[/latex]
or rearranging so that all of the constants are on the right side:
[latex]\frac{d^2x}{dt^2}=-\frac{c}{m}x[/latex]
Think carefully about what this equation implies. [latex]x[/latex] is not just a number: it is a function of time, [latex]x(t)[/latex]. The equation demands that at any time during the motion, the second time derivative of the function [latex]x(t)[/latex] must be proportional to the function [latex]x(t)[/latex] with a negative proportionality constant. Not just any function [latex]x(t)[/latex], can satisfy this restriction!
Unfortunately, without a course in differential equations, the only way that you can find [latex]x(t)[/latex] is trial and error. You could take a guess at a function, [latex]x(t)[/latex]. You could then evaluate the left side and the right side of the equation (a) and see if they are equal. If they are, then you have found [latex]x(t)[/latex]. If not, you’ll have to try a different function. (“Try again, fail again, fail better.” Samuel Beckett)
c) Guess at a mathematical form of [latex]x(t)[/latex]. See if your function satisfies the condition that its second derivative is proportional to the negative of the function.
d) What is the significance of the constant [latex]c/m[/latex] to your function?
e) Summarize your argument by completing the following sentence: “If a net linear restoring force acts on an object, the object will …”
Exercise 2
On your desk, you should have a cart that has magnets at both ends. If the cart is placed between magnetic bumpers on the track, it can be made to oscillate. The position of the cart can be monitored with a motion sensor, and the force acting on the cart, through an acceleration sensor attached to the cart.
Open Capstone (there should be a Capstone file titled MgnOsc in the 1CC3 folder) on the lab computer and ensure the position sensor is connected. Push the cart as close to one of the magnets as you can and then release it, observing the oscillation with Capstone. Take a look at the position vs time graph and the acceleration versus position graph.
a) Sketch the force – displacement curve in your workbook. Is it linear? Is the position-time curve sinusoidal?
b) Is there any region of the force-displacement curve which is approximately linear? Set the cart oscillating and use Capstone to observe the position-time curve until the cart comes to rest. Where in this data would you look for an oscillation which is confined to the linear region? Predict (from the position-time plot) and measure (from the force-displacement plot) the period of the oscillation in the linear region.
Exercise 3
A video clip of an oscillating spring system set up on the air table is below.
a) Observe the video clip and answer the following questions:
1. In the absence of friction, what is the direction of the net force when the object is
i) At its farthest left displacement
ii) Passing through the equilibrium position
iii) At its farthest right displacement
Is the net force linear with displacement? Why or why not?
2. Now consider friction. Is the net force still linear when a constant friction force is acting? Why or why not?
b) In general, the springs might have different spring constants (k) and different natural lengths [latex](\mathcal{l})[/latex]. In equilibrium, they may be stretched by different amounts (d) as shown in the diagram below.
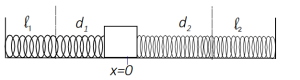
Write an expression for the force exerted by each spring when the box is displaced from equilibrium a small distance x to the right. Show that the net force is as you expect and predict the oscillation frequency.
c) Why is it difficult to write a single (net) force equation which includes friction?
d) The position-time and force-displacement data for this demonstration have been measured and can be found in the file Oscillations_Data. You should be able to predict the oscillation period of the system and compare it to the measured period.
Congratulations on completing Lab 9!
