"

Procedure

Characterizing the apparatus

All trials of this experiment will consist of the driving mass being released from a height, causing the crossbar to rotate. Set up the apparatus as shown in Figure 1, but without m_1 and m_2 attached to the crossbar. The driving mass should consist of two parts: the pan and hook, which weighs 50 g on its own, and an extra 50 g mass on top, for a total of 100 g. Make sure to use the full 100 g set-up for the entire experiment.

Drop height

It is crucial to release the hanging from roughly the same height for every trial in this experiment. Here we describe how to measure that height.

Let the cord unwind fully so that the driving mass rests stationary just above the floor. Attach a metre stick vertically to the table with masking tape, and then measure the height that the mass rests at. Record this vertical position from the metre stick on your report. Do not forget to estimate an uncertainty on this measurement, and all measurements from the metre stick. Then, wind up the cord by spinning the rotating arms until the bottom of the driving mass sits level with the lower edge of the table top [1]. This is the height/position you will drop the mass from for all trials. Measure and record this position that you will drop the driving mass from in your report.

With these measurements, calculate the distance that the driving mass will fall in your experiment, with uncertainty. Record this sample calculation in your report, and the results of the calculation in the h_0 and \delta h_0 columns in the “\mathbf{I_0} Calculation” page of the Capstone workbook. You only need to use the first row of this table.

Report of driving mass positions: 0.25 marks each
Sample calculation for the driving mass vertical drop distance: 0.75 marks

Radius of rotating shaft

For our experiment, we need to relate the linear motion of the falling driving mass to the rotational motion of the rotating shaft. For this, we need to know the radius of the rotating shaft, r (see Figure 1).

Unwind the cord fully so the driving mass rests at its bottom position that you measured previously, then slowly wind the apparatus up for 15 full revolutions and measure the height that the driving mass now rests at, and record this position in your report. Consider the geometry that relates the vertical distance travelled by the driving mass to the radius of the rotating shaft. Calculate the vertical distance travelled and use that to calculate r. Record this sample calculation in your report, and the results of the calculation in the r_0 and \delta r_0 columns in the “I_0 Calculation” page of the Capstone workbook. You only need to use the first row of this table.

Report of driving mass position: 0.25 marks
Sample calculation for the radius of the rotating shaft: 0.75 marks

Question 3

How will the (small, but finite) thickness of the string affect your measurement of the vertical shaft radius, r?

Secondly, recall from the pre-lab quiz that, when written in terms of our experimental variables, I is proportional to r^2. How does the finite thickness of the string affect our calculations of I?

0.5 marks

Estimating I0

The goal of this experiment is to find the moment of inertia of the rotating masses by themselves, I_m. To do this, the moment of inertia of the rotating shaft and crossbar without any extra mass, I_0, must be removed. We will experimentally measure I_0 here.

The remainder of our measurements now will involve timing how long it takes the driving mass to fall the distance h_0. There are stopwatches available, but feel free to use your phone if you prefer. When the rotating masses are not attached to the crossbar we will call these drop times t_0.

Wind the driving mass up to your previously determined drop distance h_0. Make sure the driving masses are not attached to the bar. When your group is ready, release the driving mass and time how long it takes to unwind fully. Make this timing measurement a total of 5 times, and record these times in the “Table 1” page of the Capstone workbook.

Copy the mean as t_0 and standard deviation as \delta t_0 to the table on the “\mathbf{I_0} Calculation” page. You only need to use the first row of this table. You should see now that the value for I_0 and its associated uncertainty are calculated [2].

Before moving on, to make the software complete later calculations automatically, you must fill each table on the “Measurement Input” page. To do this, fill in the shown values (the vertical shaft radius, drop height, and apparatus inertia, I_0) five times, in the first five rows of the table. For example, if you measured the vertical shaft radius to be r = 0.0061 \pm 0.0003 m, then you should fill in the left column of that table with 0.0061 in the first five rows and the right column with 0.0003 in the first five rows. The numbers in the columns should be identical. These will be used to compute I_m on the “Table 3” page.

Estimating Im

Now you will experimentally measure the moment of inertia of the masses, m, placed on the crossbar at several distances, R, from the axis of rotation. The value of m, including the two 0.1 kg disk-masses and the nuts used to attach them to the cross bar, is 0.2375 \pm 0.0001 kg.

We will be measuring the moment of inertia at five distances:

    \[R = 0.15 m, R = 0.125 m, R = 0.1 m, R = 0.075 m, R = 0.05 m.\]

Pick a starting distance, say R = 0.15 m, and use a ruler or metre stick to help place the centre of the disk-masses at this distance from the centre of the rotating shaft and secure them with the screw nuts. Carry out the same procedure as in Section 2.2 for measuring the moment of inertia. That is, set up the driving mass to your drop height h_0, and time the amount of time it takes the mass to fall. Repeat this timing measurement 3 times, and record the times in Table 2a in the “Table 2” Capstone page.

Then, repeat this for the other five disk-mass crossbar distances, R, recording 3 drop times for each Rin the other Tables 2b-3e.

Fill in Table 3 in the Capstone workbook with the values of R you used [3] and the associated average times with their uncertainties (i.e. standard deviations) from Tables 2a-e. The moment of inertia of the masses, I_m, will be automatically calculated and filled out in this table, along with the associated uncertainty, using Equation 4 and Equations 5 through 9.

 

Question 4

Looking at Tables 2 a-e, do you observe any correlation between the drop times (t) and the position of the disk-masses (R)? In other words, how does t vary as R increases? Provide a brief explanation for this trend based on the torque exerted on the rotating apparatus and its moment of inertia.

Hint: Think about the source of torque, which makes the shaft rotate. Is it the driving mass, or the disk-masses on the crossbar

0.5 marks

Graphical analysis

Figure 1 in the “Linear Plot” Capstone page will automatically graph your estimates of I_m, with uncertainties, on the y-axis and the square of the distance from the rotation axis, R^2, on the x-axis. Doing this will make a quadratic relation like Equation 1 appear as a straight line. The slope and y-intercept for the best-fit line are also provided.

Using the same method as in the first experiment, following Section 3.6 in the reference material manual, estimate the uncertainties on the slope and y-intercept with the help of the tables and figures in the “Linear Plot Uncertainties” sheet of the data workbook. Note, we ignore uncertainties on R in this experiment, so the analysis here only involves uncertainties/error bars in I_m. Include the best-fit-line equation, with uncertainties and proper significant figures, in the associated section of your report. When reporting your final result, please do so as an equation of the form

                                                                        

    \[y = (m \pm \delta m \text{unit}) x + (b \pm \delta b \text{unit}),\]

and remember to switch to variables you used in your hypothesis. It is fine to leave off units for values that are not supposed to have units, but make sure to include units if they should be there.

Sample calculation for the linear fit slope and y-intercept uncertainties:0.75 marks
Report of the linear fit equation: 0.25 marks

 

Question 5

Do the slope and y-intercept agree with the theoretical predictions?(Recall: The mass of the two 0.1 kg disk-masses and the nuts used to attach them to the cross bar in total is 0.2375 \pm 0.0001 kg)

1.0 marks

Question 6

Explain how the finite sizes of your masses m_1 and m_2 affect the moment of inertia of the system, and how this is related to the y-intercept in the I_m versus R^2 plot. (Hint: In the theoretical expression from Equation 2, if all the mass in the masses m_i is located exactly at R_i = 0 for all i, then I_m = 0.)

0.5 marks

Question 7

Some of the uncertainty in I_m comes from I_0. How does this uncertainty affect the scatter of the data points? That is, does the uncertainty in I_0 affect all data points the same way?

0.5 marks

Digital submission (2 marks total):
Figure 1: 0.5 marks
Figure 2a,b: 1.0 marks
Capstone Workbook: 0.5 marks

Saving your Capstone workbook

Here we discuss how and where to store the results from your Capstone workbook for marking. If any of the following instructions are unclear, be sure to double-check that you are doing this correctly with your TA.

To save your work, we will make use of the “snapshot” feature in the Capstone software.

A snapshot of each page can be recorded with the following steps:

  • Click the drop-down arrow next to the camera button near the top of the screen.
  • Make sure the “Snapshot Workbook Page Content” option is selected.
  • Click the camera button. This will take a snapshot of the current workbook page.

The yellow button to the right of the camera button that looks like a book will display the “Journal,” which is an area within the Capstone software that stores the snapshots as they are taken. This button merely toggles the display of the journal within the software window. All snapshots will be stored to the journal whether this button is active or not. Be sure to check the Journal to ensure you have taken a snapshot of every page of your workbook. Note: This includes the page with your names and student numbers! If you would like to delete a snapshot, you can do so by clicking on the snapshot, then clicking on the red “x” button at the top of the journal window.

When your journal is complete, you are ready to export your snapshots. Export your Journal by finding the icon in the Journal window near the top that looks like a folder with a small arrow pointing to it. If you hover the mouse cursor over the icon but don’t click, it should say “Export to HTML”. Click this button, and be patient if nothing happens immediately–sometimes this action takes several moments. When the software is ready, a File Explorer window will open on the screen, and you will be asked to select a folder to export the Journal to. Navigate to the Desktop, enter the folder that corresponds to your Lab section, and then the workstation number that you are at. Once you have successfully exported your Journal, the File Explorer window will close.

Finally, before you leave the lab, find your exported Journal by opening a new File Explorer window and navigating into the folder/directory that you exported to. You should see a folder with the name of the experiment–specifically, the name of the Capstone software file. Within this folder should be one HTML file and a series of PNG images, one for each of your Capstone workbooks. These images will make up the digital portion of your lab submission. Double check with your TA that your snapshots have been taken properly before you leave.

  1. This exact choice of set up is arbitrary; you could instead use the top of the driving mass as the reference/measurement point. What is important is to be consistent, and use the same reference point in very trial. ↵
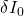  2. This calculation uses Equations 5 through 9 from Section 3. Recall that these calculations for I_0 and \delta I_0 were part of the pre-lab quiz. ↵
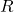  3. For the sake of simplifying the experiment, we ignore uncertainties on R ↵

License

PHYSICS 1AA3 - LABORATORY EXPERIMENTS Copyright © by Physics 1AA3 Team. All Rights Reserved.

Share This Book