Background theory for calculating moment of inertia
In this experiment, the gravitational potential energy (![]() ) of a falling mass is converted into the translational kinetic energy (
) of a falling mass is converted into the translational kinetic energy (![]() ) of this mass and the rotational kinetic energy of the crossbar system. The conservation of energy principle requires that the initial total energy (
) of this mass and the rotational kinetic energy of the crossbar system. The conservation of energy principle requires that the initial total energy (![]() plus
plus ![]() ) be equal to the total final energy (
) be equal to the total final energy (![]() plus
plus ![]() ), provided frictional forces are negligible.
), provided frictional forces are negligible.
The initial conditions for the system just before the driving mass is released are:
- The system is at rest, so
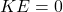 .
. - We define the final (lowest) position of the driving mass
 as the zero point for the
as the zero point for the 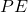 , so the initial
, so the initial 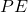 is
is 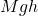 , where
, where 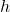 is the initial height of the mass above the final height.
is the initial height of the mass above the final height. - Combining the two points above means the initial total energy is
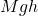 .
.
Laying out the final conditions for the system we have:
- The driving mass has translational
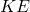 ,
, 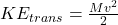 , where
, where  is the final speed.
is the final speed.
- The rotating apparatus has rotational KE,
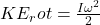 , where
, where 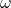 is the final angular speed.
is the final angular speed. - The driving mass has
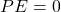 .
. - Tallying up the energies gives the final total energy:
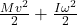 .
.
Conservation of energy requires
(5) ![]()
be true. If ![]() and
and ![]() can be determined for the system, then Equation (5) can be used to calculate the moment of inertia. To calculate
can be determined for the system, then Equation (5) can be used to calculate the moment of inertia. To calculate ![]() from
from ![]() , the time it takes for
, the time it takes for ![]() to fall the distance
to fall the distance ![]() , we use the constant acceleration formulae
, we use the constant acceleration formulae
(6) ![]()
and
(7) ![]()
knowing that ![]() here to obtain
here to obtain
(8) ![]()
Finally, since the string around the shaft has the same speed as the driving mass ![]() ,
,
(9) ![]()
where ![]() is the radius of the vertical, rotating, shaft.
is the radius of the vertical, rotating, shaft.
