Warm-Up: Let’s go snorkelling
Light and Snell's Law: Warm-up
The speed of light in a vacuum is one of the universe’s fundamental constants, measuring approximately 3.0 x 108 m/s. However, the speed of light can vary depending on its medium. For example, the speed of light in a vacuum is not the same as the speed of light in glass. A parameter that describes how much a medium slows the speed of light is the Index of Refraction:
[latex]n=\frac{c}{v}[/latex]
In this equation, c is the speed of light in a vacuum, and v is the speed of light through a medium (like air or water). Therefore, the index of refraction (n) is a dimensionless value that is related to how fast light moves in a certain medium. For reference, the refractive index of air is nearly n = 1, while the refractive index of glass is around n = 1.5 - 1.9. Some materials (like diamond) have an index of refraction greater than 2.
Think about it:
What is the range of possible values for an Index of Refraction? Can you have n < 1?
A consequence of light having different speeds in different media is that the trajectory of the beam will be bent, or 'refracted'.

Take for example Hamlet's snorkelling in the image below.
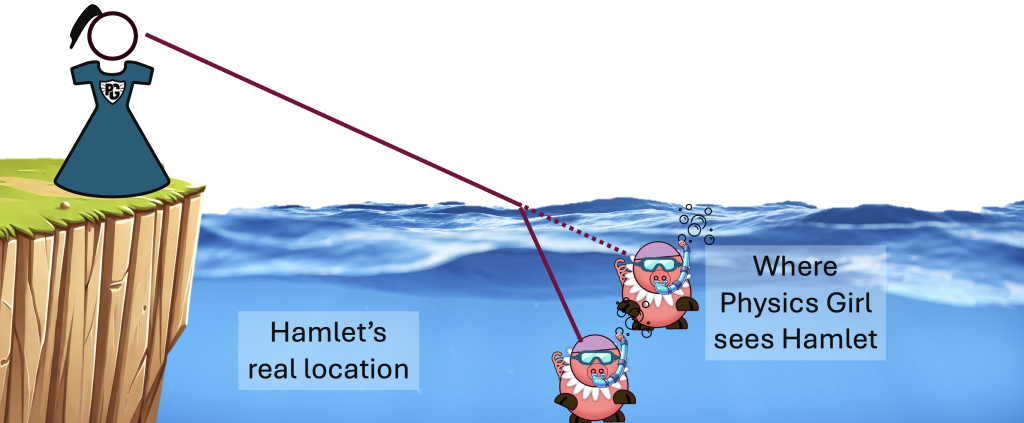
Hamlet's real location is labeled in the image. But this is not where Physics Girl sees Hamlet due to the bending of light. The dotted line is Hamlet's apparent location - what Physics Girl sees. Light maintains a straight trajectory in both air and water, but at the boundary of two media, will bend by some angle. This creates an 'apparent location' of the Hamlet that Physics Girl sees (the dotted line), which is different from the actual location of Hamlet (solid line).
The path the light takes (what Physics Girl sees) is shown in the figure below:
 The angle of incidence (θinc) and the angle of refraction (θref), as measured relative to a normal line (dotted line) perpendicular to the surface, are related by the refractive index of each medium, and are described by Snell’s Law,
The angle of incidence (θinc) and the angle of refraction (θref), as measured relative to a normal line (dotted line) perpendicular to the surface, are related by the refractive index of each medium, and are described by Snell’s Law,
[latex]n_1\sin\theta_{inc} =n_2\sin\theta_{ref}[/latex]
Where n1 is the index of refraction of the first material and n2 is the index of refraction of the second material. In the image above, the first material is air (n=1) and the second is water (n=1.33).
Think about it:
Based on the schematic and what you know about indices of refraction, does Physics Girl need to aim above or below the apparent location of Hamlet when tossing him a flashlight?
A brief history of optics:
Snell’s Law is named after the Dutch astronomer Willebrord Snellius who wrote this equation in 1621, however, this law actually goes back to at least 984, when the Persian scientist Ibn Sahl used it to calculate the shape of lenses! Fast forward to 2018, our McMaster Alumna Prof. Donna Strickland became the third woman to win the Nobel Prize for Physics for her work in optics.
In the following exercises, you will measure n and learn how to obtain the angle of refraction of light as it passes through different media.
Before you continue!
Make sure you are familiar with Snell's Law and refraction, as these concepts will be used in the later exercises.

