Exercise 3: Measuring angles of refraction and index of refraction
In the last exercise, you observed light being ‘refracted’, causing the bottom half of your markers to appear shifted. Let’s try to quantify how much the light is refracted at the interface.
Continue filling your clear container with water until it is almost full, then look along the same line of sight you marked with your markers. While keeping the markers on the far side of the box lined up, stick two more markers on the side of the box closest to you such that they also line up with your perceived line of sight. From this perspective, it should appear that all of your markers are in one line.
Exercise 3.1 (2 marks)
Submit a picture of your experimental set-up taken from above. Your photo must clearly show the location of the student card(s) of the participating member(s) in this lab, along with your 4 markers, box, and the 45 degree line of sight you drew in Exercise 2.
Secondly, provide an additional image of the student card(s) used in the previous photo. Here, the student name(s) and student number(s) must be legible. With your experimental set up in the background, you may take this image from a closer view to ensure the student card(s) is/are in full focus. Note: you do not need to be in the photo. If you are completing this lab with others virtually, you may provide a screenshot of your video call, with the student cards of all members visible. Your experimental set up must still be visible in the background.
Remove your box (careful not to spill) and inspect the lines of sight marked by your markers. Draw lines alongside the markers as shown in the diagram below.
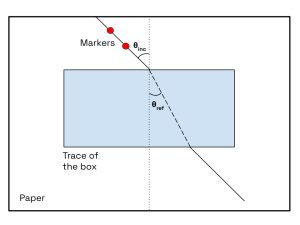 Note: Since the edges of the box are parallel, the diagonal lines above and below the box are also parallel to one another. However, these lines do not form a straight line as they are shifted due to refraction.
Note: Since the edges of the box are parallel, the diagonal lines above and below the box are also parallel to one another. However, these lines do not form a straight line as they are shifted due to refraction.
By further following the video from Exercise 2, you should be able to measure the angle of incidence and the angle of refraction of light passing through your water-filled box:
Note: If you would like to view this video in full screen, you can click on the McMaster logo found in the bottom right corner (this opens the video in a new tab).
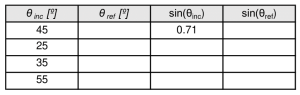
Fill in the first row of the table below. This table can be found on the second tab of the Excel sheet provided in Exercise 1 of this lab.
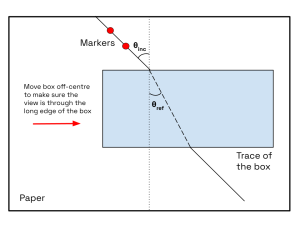
 Now, repeat this experiment for incident angles of 25, 35 and 55 degrees. Keep in mind, you will have to re-draw your line of incident angles for every new angle. You may find that for an angle of incidence of 55 degrees, you may need to move the box such that your line of sight is still through the long edge of the box (see image below):
Now, repeat this experiment for incident angles of 25, 35 and 55 degrees. Keep in mind, you will have to re-draw your line of incident angles for every new angle. You may find that for an angle of incidence of 55 degrees, you may need to move the box such that your line of sight is still through the long edge of the box (see image below):
Exercise 3.2 (2 marks)
Exercise 3.3 (4 marks)
i) Similarly to Exercise 1.2, create a plot of sin(θref) vs sin(θinc). Draw a line of best fit, and use it to calculate n1/n2.
ii) Based on your line of best fit, assuming that the refractive index of air is n = 1.00, what is the refractive index of water?
Exercise 3.4 (2 marks)
Before you continue!
Before continuing, be sure you have completed (3.1) to (3.4), which will be graded and submitted through Crowdmark.

