Exercise 1: Energy conservation of a bouncing ball
In this lab you will be exploring energy conservation during collisions. You will do this by studying how a ball bounces (‘collides’) on different surfaces, and by calculating the energy lost (to sound, to friction, etc.) from each collison with the ground.
In the Warm-up exercise you considered how high a ball would bounce if it was dropped from a certain height. For example for a perfect elastic collision with the floor and no air resistance, if you were to drop the ball from a 1 m height, it would bounce back up to a height of 1 m, and all the mechanical energy of the ball would be conserved. So, in this example of a perfectly elastic collision, the ball would bounce back to its initial height, and the kinetic energy of the system, in this case the ball and the floor, is the same before and after the collision.
Exercise 1.1 (2 marks)
Assume half of the mechanical energy is lost during a bounce, and fill in the following chart (three highlighted cells) as the ball is released from rest, just the moment before the ball collides with the ground and the moment just after the ball leaves the ground. Notice that your answers will be written using variables.
|
|
Kinetic Energy |
Potential Energy |
Speed |
|
Just-released (y = h) |
0 |
mgh |
0 |
|
Just before impact (y = 0) |
½ mv12 |
0 |
v1 = ? (write in terms of g and h) |
|
Just after impact (y = 0) Hint: half the energy is lost |
K = ? (write in terms of variables m and v1) |
0 |
v2 = ? (write in terms of variable v1) |
You will find in the following Exercises, that real-life collisions do not conserve all the mechanical energy and they are not perfectly elastic. In Figure 1.1 below the height as a function of time is shown for a perfectly elastic bouncing system; the height of the ball always returns to the initial height of the drop. Note that while the ball is in the air we are assuming zero energy loss; we are ignoring air resistance.
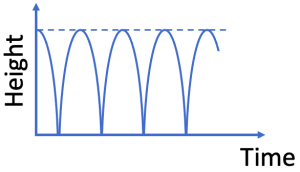
Figure 1.1 is not realistic and not exactly what you will see in your experiments. Your experimental results will show that the time between bounces gets smaller and the maximum height reduces with each bounce. The collisions with the ground are not perfectly elastic. This is shown in Figure 1.2 below.
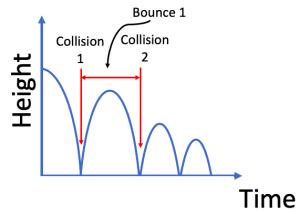
The goal of the following experiments is to determine how elastic the bouncing of your ball is. You can accomplish this by calculating the maximum height of a bouncy ball (potential energy) on multiple bounces and from this height, calculate the speed (kinetic energy) the ball left the surface with.
Unfortunately, measuring the height of successive bounces and maximum velocities is difficult (yes, you could do it using the video method you used in Lab 1, but it would be really tedious). Instead, you will do it by measuring the time between collisions on an audio track.
If an object leaves the ground with a speed v0 and is only under the influence of gravity (no air resistance), you can calculate how long it will be in the air until it reaches the ground again.
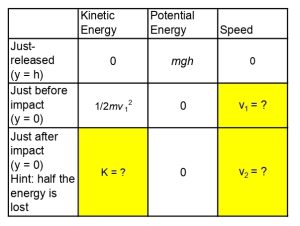
Exercise 1.2 (1 mark)
Use the following kinematic equation to derive an equation that tells you how long the ball is in the air, Δt, if it left the ground with a speed 
straight up, and returned to the ground with the same speed :
Helpful hints: Remember, we have defined the ground as y = 0 m (which is both the initial and final position). Assume up is positive so that the acceleration due to gravity is g = -9.8 m/s2.
Pick the correct answer directly on Crowdmark.
Exercise 1.3 (1 mark)
A ball is bounced off the ground, goes straight up into the air, and falls back down to the ground. It is in the air for a time Δt. Use the following kinematic equation to derive an equation that tells you the speed that a ball leaves the ground with:
Helpful hints: Remember, we have defined the ground as y = 0 m (which is both the initial and final position). Assume up is positive so that the acceleration due to gravity is g = -9.8 m/s2.
Pick the correct answer directly on Crowdmark.
The equations you derived tell you how long the ball is in the air based on its speed as it leaves the ground, or alternatively, if you know the time the ball is in the air between collisions you can determine the speed the ball left the ground with. Of course, if you know the speed, you also know how much kinetic energy it had as it left the ground.
Before you continue!
Before continuing, be sure you have completed (1.1), (1.2), and (1.3) which will be graded and submitted through Crowdmark.
