Exercise 1: Designing the experiment
Like in previous experiments, your task is to measure a parameter that may seem unconventional to record. The index of refraction describes the speed of light through a medium. However, you won’t be able to measure displacement over time like in Lab 1 (light is waaaaay faster than your camera’s frame rate). Since you can’t measure the speed of light in various media directly, you can determine the index of refraction indirectly using Snell’s Law. You will work out how to do this below.
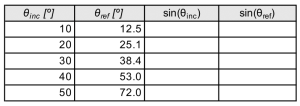
Snell’s Law is a great equation; two sides, four variables, one sweet sweet principle. That means, in order to solve for the refractive index of your chosen medium (n2), you need to know θinc , θref , and n1. To get familiar with this great equation, consider the following chart of experimental data:
Below is the link to download the Excel file that you may use for Lab 4 (for Exercise 1 and Exercise 3). The first tab includes the table for Exercise 1 (seen above), while the second tab has the table you will be using for Exercise 3.
The experimental set up is exactly like the picture of Physics Girl and Hamlet snorkelling (light travels from the first material into a second material at angle θinc, and is refracted at an angle θref as it travels through the second material). However, there is a key difference: the materials are not air and water. Thus, their refractive indices are unknown. Fortunately, this data can be used to determine the ratio between the two material’s refractive indices (n1/n2). In the next section, you will do exactly that.
Exercise 1.1 (1 mark)
Calculate sin(θref) and sin(θinc) for the values in the table above, and submit your table.
Exercise 1.2 (1 mark)
a. The first material has a higher refractive index since [latex]\sin{(\theta_{ref})} < \sin{(\theta_{inc})}[/latex] therefore [latex]n_{inc} > n_{ref}[/latex]
b. The first material has a higher refractive index since [latex]\sin{(\theta_{ref})} > \sin{(\theta_{inc})}[/latex] therefore [latex]n_{inc} > n_{ref}[/latex]
c. The second material has a higher refractive index since [latex]\sin{(\theta_{ref})} < \sin{(\theta_{inc})}[/latex] therefore [latex]n_{ref} > n_{inc}[/latex]
d. The second material has a higher refractive index since [latex]\sin{(\theta_{ref})} > \sin{(\theta_{inc})}[/latex] therefore [latex]n_{ref} > n_{inc}[/latex]
Exercise 1.3 (3 marks)
i) Create a plot of sin(θref) vs sin(θinc) from your table. Hint: remember that this means that sin(θref) is on the y-axis.
ii) Draw and calculate a line of best fit. Show the equation of the line of best fit on your plot.
iii) Use your line of best fit to calculate n1/n2.
iv) If n2 = 1.33, what is n1?
Exercise 1.4 (2 marks)
If you extend your line of best fit you will see that the line goes through the point of sin(θref) =1.
i) What is the refracted angle at this point?
ii) What is the incident angle?
Choose the correct answer(s) on Crowdmark.
a. i) [latex]\theta_{ref} = 90^\circ[/latex] ii) [latex]\theta_{inc} = 1.24^\circ[/latex]
b. i) [latex]\theta_{ref} = 1.24^\circ[/latex] ii) [latex]\theta_{inc} = 90^\circ[/latex]
c. i) [latex]\theta_{ref} = 90^\circ[/latex] ii) [latex]\theta_{inc} = 53.6^\circ[/latex]
d. i) [latex]\theta_{ref} = 53.6^\circ[/latex] ii) [latex]\theta_{inc} = 90^\circ[/latex]
Exercise 1.5 (1 mark)
If you continue to increase θinc what happens to sin(θref)? Hint: Can you have sin(θref) > 1? This is called Total Internal Reflection, and an important concept in designing optical fibres.
In the next exercises, you will perform an experiment and use Snell’s Law to determine the index of refraction of water.
Before you continue!
Before continuing, be sure you have completed (1.1) to (1.3), which will be graded and submitted through Crowdmark.