17.2 Reliability Metrics
As introduced earlier in this chapter, reliability is a measure of how consistently a system, product, or service performs its intended function without failure over a specified time period. To quantify this, several key reliability metrics are used. These metrics help evaluate performance, identify areas for improvement, and guide design and maintenance decisions.
Failure Rate Percentage(%)
This basic metric expresses the proportion of failed units relative to the total number tested, typically over a defined time period. It is calculated using the formula:
Example:
Magtis Electric tested 1,000 light bulbs overnight. If 20 bulbs failed, the failure rate is:
Failure Rate (λ)
The failure rate, denoted by λ, represents the rate at which a product or system fails over time. It applies to both repairable and non-repairable items and is typically expressed as failures per unit time.
Example:
Magtis Electric tested 30 hair dryers designed to operate continuously for 1,000 hours. If 10 units failed at various times, the failure rate can be calculated using the total operating time and the number of failures.
| Tested Units | Unit 1 | Unit 2 | Unit 3 | Unit 4 | Unit 5 | Unit 6 | Unit 7 | Unit 8 | Unit 9 | Unit 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Failed after | 500 | 550 | 600 | 450 | 780 | 680 | 350 | 410 | 720 | 370 |
Based on the above failure data, the failure rate of this product is:
The above number does not reveal a meaningful measure of the reliability of this product for its user. The users buy this product because they expect the product to last for 1000 hours if used continuously. Using the failure rate, however, a more meaningful reliability measure can be obtained in terms of MTTF and MTBF. These two measures are reviewed in more detail.
Note: The raw failure rate alone may not provide meaningful insight for users. More informative metrics, such as MTTF and MTBF, are derived from it.
Mean Time to Failure (MTTF)
MTTF is used for non-repairable items (e.g., batteries, light bulbs). It represents the average time until failure and is calculated as:
This metric helps estimate how long a product is expected to function before failing.
Mean Time Between Failures (MTBF)
MTBF applies to repairable systems (e.g., refrigerators, industrial machines). It measures the average time between successive failures, including the time taken for fault diagnosis and repair.
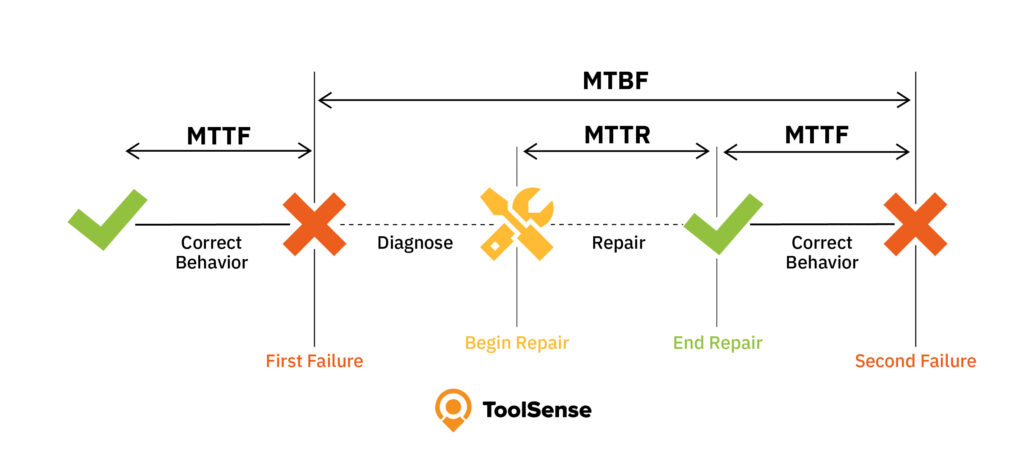
Image Description
This image illustrates a timeline of a system's operation and maintenance cycle, highlighting different stages of performance and repair. The timeline is divided into several sections, marked by symbols and labels:
- Correct Behaviour - The system is operating normally.
- First Failure - The point at which the system fails.
- Diagnose - The phase where the issue is identified.
- Begin Repair - The start of the repair process.
- Repair - The phase of fixing the issue.
- End Repair - Repair is completed, and normal operation resumes.
- Correct Behaviour - The system is back to normal operation.
- Second Failure - The next failure point of the system.
Additional labels and arrows indicate time intervals:
- MTTF (Mean Time to Failure) - The average time between the start of normal operation and a failure.
- MTBF (Mean Time Between Failures) - The average time between two consecutive failures.
- MTTR (Mean Time to Repair) - The time taken to diagnose and repair the system after a failure.
The formula is:
[latex]\begin{align*}\text{MTBF} = \theta = \frac{\text{Operating Time (Cycles)}}{\text{Number of Failures}}\end{align*}[/latex]
Relationship Between MTBF/MTTF and Failure Rate
Both MTTF and MTBF are statistical predictions based on historical data. They do not guarantee failure-free operation but provide useful estimates of expected performance. Importantly, they are inversely related to the failure rate:
[latex]\begin{aligned} \text{MTTF \& MTBF} &= \theta = \frac{\text{Operating Time (Cycles)}}{\text{Number of Failures}} \\[8pt] \text{FR} &= \lambda = \frac{\text{Number of Failures}}{\text{Operating Time (Cycles)}} \\[10pt] \textbf{OR} \\[6pt] \text{MTTF \& MTBF} &= \theta = \frac{1}{\lambda} \end{aligned}[/latex]
Example Revisited: Hair Dryer Reliability
If the failure rate λ = 0.000394, then:
This means the average time between failures for the hair dryer is approximately 2,538 hours. If customer expectations exceed this value, the manufacturer may need to revise the design. If expectations are lower, the product has exceeded performance standards (Haney, 2021).
For further explanation, refer to this instructional video:
Video: "What is MTBF and How to Calculate | Mean Time Between Failure" by LeanVlog [1:53] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
