15.4 Resource Assignment in Operations Scheduling
In earlier sections, we explored how jobs are scheduled across multiple machines. However, in some operational settings, resources must be assigned on a one-to-one basis—for example, assigning a specific crane to a construction site or a worker to a particular task. In such cases, the objective is to assign each resource to exactly one job in a way that minimizes total cost or time.
This type of problem is solved using a specialized version of the transportation model known as the Hungarian Method (also referred to as the Kuhn-Munkres Algorithm). Unlike general transportation problems, the Hungarian Method ensures that each resource is assigned to exactly one job, and each job is assigned to exactly one resource.
Example: Crane Assignment Problem
A construction firm is working on four sites (A, B, C, and D) and has four cranes (1, 2, 3, and 4). The time (in weeks) it takes each crane to complete work at each site is shown in the cost matrix below. The goal is to assign each crane to one site such that the total time of crane usage is minimized.
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 14 | 5 | 8 | 7 |
| 2 | 2 | 12 | 6 | 5 |
| 3 | 7 | 8 | 3 | 9 |
| 4 | 2 | 4 | 6 | 10 |
See the process below to apply the Hungarian Method.
Step 1: Row Reduction
- Identify the minimum value in each row and subtract it from all elements in that row.
- This ensures that each row has at least one zero.
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 8 | 0 | 2 | 2 |
| 2 | 0 | 9 | 4 | 3 |
| 3 | 4 | 4 | 0 | 5 |
| 4 | 0 | 2 | 5 | 7 |
Step 2: Column Reduction
- For each column, subtract the minimum value in that column from all elements.
- This ensures that each column also has at least one zero.
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 8 | 0 | 2 | 0 |
| 2 | 0 | 9 | 4 | 1 |
| 3 | 4 | 4 | 0 | 3 |
| 4 | 0 | 2 | 5 | 5 |
Step 3: Cover All Zeros with Minimum Number of Lines
- Use horizontal lines through Row 1 and vertical lines through Column 1 to cover all zeros in the matrix.
- Vertical line through Column 3
- If the number of lines is less than the matrix dimension (n = 4), proceed to adjust the matrix.
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 8 | 0 | 2 | 0 |
| 2 | 0 | 9 | 4 | 1 |
| 3 | 4 | 4 | 0 | 3 |
| 4 | 0 | 2 | 5 | 5 |
Step 4: Matrix Adjustment
- Find the smallest uncovered value (k). k = 1 (Row 2, Column 4)
- Subtract k from all uncovered elements.
- Add k to elements at intersections of lines.
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 9 | 0 | 3 | 0 |
| 2 | 0 | 8 | 4 | 0 |
| 3 | 4 | 3 | 0 | 2 |
| 4 | 0 | 1 | 5 | 4 |
- Repeat Steps 3 and 4 until the number of lines equals the matrix dimension.
Step 5: Zero Crossing for Matrix Adjustment / Optimal Assignment
- Select zeros such that no row or column contains more than one assignment.
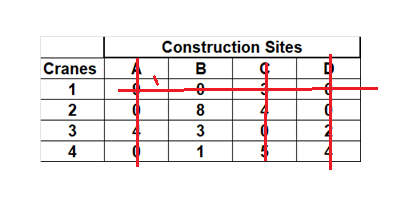
15.4.6 Image Description
The image (15.4.6) depicts the following table with red lines crossing out columns corresponding to construction sites A, C, and D, as well as row 1.
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 9 | 0 | 3 | 0 |
| 2 | 0 | 8 | 4 | 0 |
| 3 | 4 | 3 | 0 | 2 |
| 4 | 0 | 1 | 5 | 4 |
- If multiple zeros exist in a row or column, choose the one that allows for a complete assignment.
| Construction Sites | ||||
|---|---|---|---|---|
| Cranes | A | B | C | D |
| 1 | 0 | 0 | ||
| 2 | 0 | 0 | ||
| 3 | 0 | |||
| 4 | 0 | |||
To decide which four zeros must be selected, we need to consider that no crane can be assigned to more than one site. Therefore, if we have only one zero under any site, that zero would be selected. If we have more than one zero, we have to decide which one to assign
Final Assignment and Result
After applying the Hungarian Method, the optimal assignments yield a cost of 140 and as shown below:
- Crane 1 → Site B
- Crane 3 → Site C
- Crane 4 → Site A
- Crane 2 → Site D
Crane 2 can be assigned to Site A and Site D. If we assign it to Site A, Crane 4 cannot be assigned to any site. So, Site A, which can take Cranes 2 and 4, would take Crane 4, and Crane 2 would be assigned to Site D, as shown below.
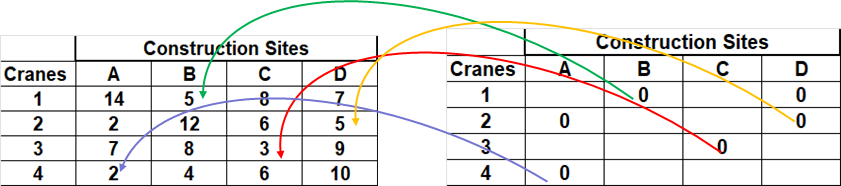
15.4.8 Image Description
The image features two tables connected by coloured arrows, each representing the allocation of cranes to construction sites. Here are the descriptions of the tables and arrows:
| Construction Sites | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 14 | 5 | 8 | 7 |
| 2 | 2 | 12 | 6 | 5 |
| 3 | 7 | 8 | 3 | 9 |
| 4 | 2 | 4 | 6 | 10 |
| Construction Sites | ||||
|---|---|---|---|---|
| Cranes | A | B | C | D |
| 1 | 0 | 0 | ||
| 2 | 0 | 0 | ||
| 3 | 0 | |||
| 4 | 0 | |||
Arrows connect values in the first table to the corresponding allocations in the second table:
- A green arrow originates from a 0 value in Table B under crane 1, site B pointing to crane 1, site B, with the value 5 in, Table A.
- A yellow arrow originates from a 0 value in Table B under crane 2, site D pointing to crane 2, site D, with the value 5, in Table A .
- A red arrow originates from a 0 value in Table B under crane 3, site C pointing to crane 3, site C, with the value 3, in Table A.
- A blue arrow originates from a 0 value in Table B under crane 4, site A pointing to crane 4, site A, with the value 4, in Table A.
This assignment yields a minimum total time of 15 weeks, calculated as:
Total Time =2 (Crane 1) + 5 (Crane 3) + 3 (Crane 4) + 5 (Crane 2) = 15 weeks
This example illustrates how the Hungarian Method provides an efficient and systematic approach to solving one-to-one resource assignment problems in operations scheduling.

