"

12.5 Solving a Transportation Problem Using the Simplex Method in Excel Solver

In Chapter 11, we solved a transportation problem using the Stepping Stone and MODI methods. We will now revisit the same problem and solve it using the Simplex Method via Excel Solver.

Initial Transportation Cost

Using the initial basic feasible solution, the firm’s transportation cost is calculated as follows:

Figure 12.5.1 Transportation Table
M1 M2 M3
DC1 150 6 50 9 16 0
DC2 11 150 10 50 7 0
DC3 16 12 200 10 0
0 0 0

Total Cost:

150(6) + 50(9) + 150(10) + 50(7) + 200(10) = $5,200

Stepping Stone Method

Using the Stepping Stone Method, the optimal solution was found to be:

150(6) + 50(9) + 0(10) + 200(7) + 150(12) + 50(10) = $5,050

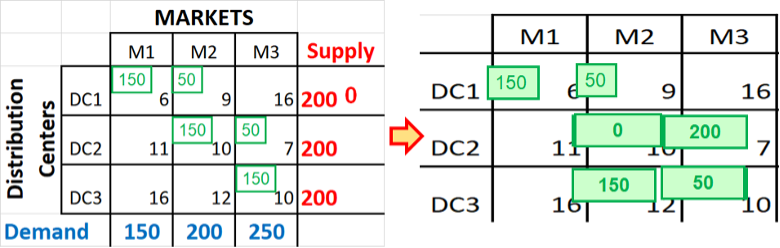
 Figure 12.5.2 Transportation Tables
12.5.2 Image Description

Two side-by-side transportation tables for a supply and demand allocation problem.

Left table: Distribution centers (DC1, DC2, DC3) are listed on the left, markets (M1, M2, M3) along the top. Each cell shows a shipping cost, with green numbers indicating allocated units. Supply is listed in red on the right (200 for each DC, with DC1 showing 0 remaining), and demand in blue along the bottom (150 for M1, 200 for M2, 250 for M3). Allocations: DC1 sends 150 to M1 and 50 to M2; DC2 sends 150 to M2 and 50 to M3; DC3 sends 150 to M1 and 50 to M3.

Right table: The same allocations are redrawn with green boxes around the numbers, visually emphasizing how shipments from DCs are distributed to meet the demands of markets.

Linear Programming Method 

We will now formulate this problem as a linear programming problem (LPP) and solve it using the Excel Solver.

Objective: Minimize total transportation cost:

Figure 12.5.3 Transportation Table
MARKETS
M1 M2 M3 Supply
Distribution Centers DC1 X11

6

 X12

9

 X13

16

 200
DC2 X21

11

 X22

10

 X23

7

 200
DC3 X31

16

 X32

12

 X33

10

 200
Demand 150 200 250

Minimize Z

[latex]Z:\; \min TC = \begin{aligned} &X_{11}(6) + X_{12}(9) + X_{13}(16) \\ &+ X_{21}(11) + X_{22}(10) + X_{23}(7) \\ &+ X_{31}(16) + X_{32}(12) + X_{33}(10) \end{aligned}[/latex]

Subject to supply constraints:

  • X11+X12+X13 ≤ 200
  • X21+X22+X23 ≤ 200
  • X31+X32+X33 ≤ 200

And demand constraints:

  • X11+X21+X31 ≤ 150
  • X12+X22+X32 ≤ 200
  • X13+X23+X33 ≤ 250

All decision variables Xij ≥ 0

Implementing in Excel

  1. Set up the cost matrix and decision variables in Excel.
  2. Use SUMPRODUCT formulas to compute the total cost and the left-hand sides of the constraints.
  3. Verify that all formulas are correctly implemented.
  4. Open Solver and configure:
    • Objective: Minimize the total cost of the cell.
    • Variable Cells: All Xij decision variables.
    • Constraints: Supply and demand constraints as listed above.
    • Solving Method: Select Simplex LP.
Figure 12.5.4
X11 X12 X13 X21 X22 X23 X31 X32 X33 Left Right
OBJE 6 9 16 11 10 7 16 12 10
D1 1 11 200
D2 1 1 1 200
D3 1 1 1 200
M1 1 1 1 150
M2 1 1 1 200
M3 1 1 1 250
SOLUTION 0 0 0 0 0 0 0 0 0

After all SUMPRODUCT formulas have been correctly implemented and verified, the model is now fully prepared for optimization. The Solver-ready layout of the transportation problem is shown below:

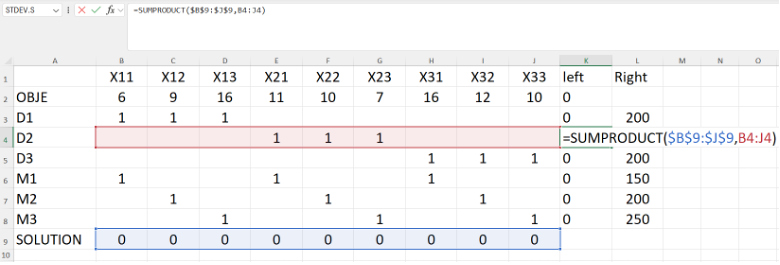
Figure 12.5.5 Excel Spreadsheet linear programming solution.Excel Screenshot. © Microsoft.
12.5.5 Image Description

An Excel spreadsheet showing a linear programming or optimization setup with decision variables, constraints, and an objective function. The columns labelled X11 through X33 represent variables, while rows D1 to D3 and M1 to M3 list constraints. Row 2 (D1) has ones under X11, X12, and X13. Row 3 (D2) has ones under X21, X22, and X23. Row 4 (D3) has ones under X31, X32, and X33. Additional rows M1 to M3 contain other combinations of ones under different variables. The "OBJE" row at the top lists objective coefficients such as 6, 9, 16, 11, 10, etc. Columns K (“left”) and L (“Right”) contain constraint results, with right-hand side values 200, 150, 200, and 250. Row 10 ("SOLUTION") currently has zeros under all variables. A formula bar shows =SUMPRODUCT($B$9:$J$9,B4:J4)

The optimized solution, as computed by Excel Solver, is presented below:

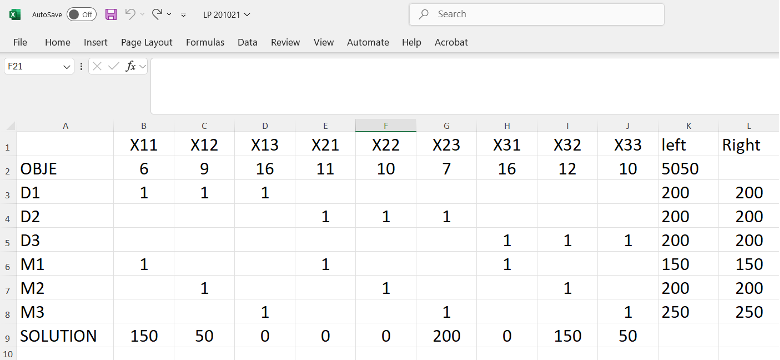
Figure 12.5.6 Excel Spreadsheet linear programming solution.Excel Screenshot. © Microsoft.
12.5.6 Image Description

An Excel spreadsheet illustrating a linear programming solution, featuring variables X11–X33, objective values, demand and supply constraints, and solution values. The final solution assigns nonzero values to X11, X12, X23, X32, and X33, achieving an objective total of 5050.

Figure 12.5.7 Transportation Table
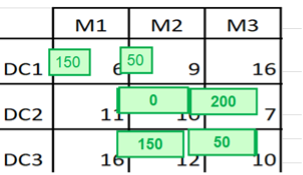
12.5.7 Image Description

A transportation table showing supply nodes (M1, M2, M3) across the top and demand centers (DC1, DC2, DC3) along the side. Each cell contains a cost value, with green boxes displaying allocated shipment quantities. Allocations are: 150 from M1 to DC1, 50 from M2 to DC1, 200 from M2 to DC2, 150 from M1 to DC3, and 50 from M2 to DC3. Other routes have no allocation.

 

Solver Output

After solving, Excel Solver returns the following optimal allocation:

[latex]150(6) + 50(9) + 0(10) + 200(7) + 150(12) + 50(10) = 5{,}050[/latex]

This matches the optimal solution previously obtained using the Stepping Stone method, confirming the validity of the Simplex-based approach in Excel.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Operations Management Copyright © 2024 by Azim Abbas and Seyed Goosheh is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book