12.2 Solving the LPP Using the Graphical Method
To solve the formulated Linear Programming Problem (LPP) graphically, we begin by converting the inequality constraints into equations. This allows us to plot the boundary lines that define the feasible region.
Given the constraints:
[latex]3x_{1} + 5x_{2} = 78 \text{(Mixer time)}[/latex]
[latex]4x_{1} + x_{2} = 36 \text{(Oven time)}[/latex]
These equations can be represented graphically by identifying their intercepts with the axes and drawing the corresponding lines. This is illustrated in Figure 12.2.1, which shows the boundary lines for the mixer and oven constraints.
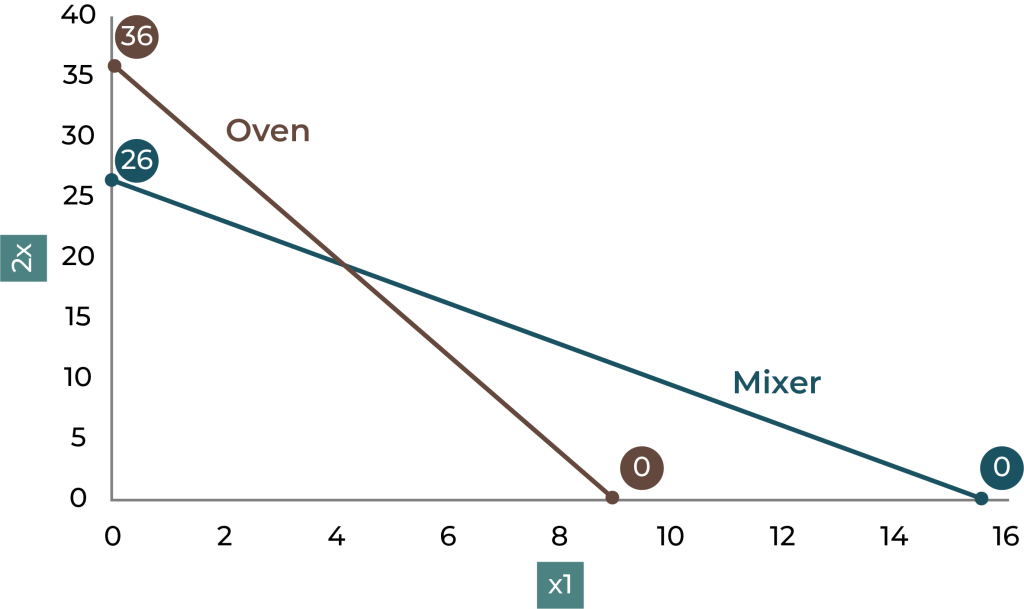
However, since the original constraints are inequalities:
[latex]3x_{1} + 5x_{2} = 78[/latex]
[latex]4x_{1} + x_{2} = 36[/latex]
We must consider not only the lines themselves but also the regions they bound. The feasible region includes all points that satisfy both inequalities simultaneously. This region is typically shaded on the graph.
In Figure 12.2.2, the individual constraint regions are shown in light brown and teal, while their intersection, representing the feasible region, is highlighted in grey.
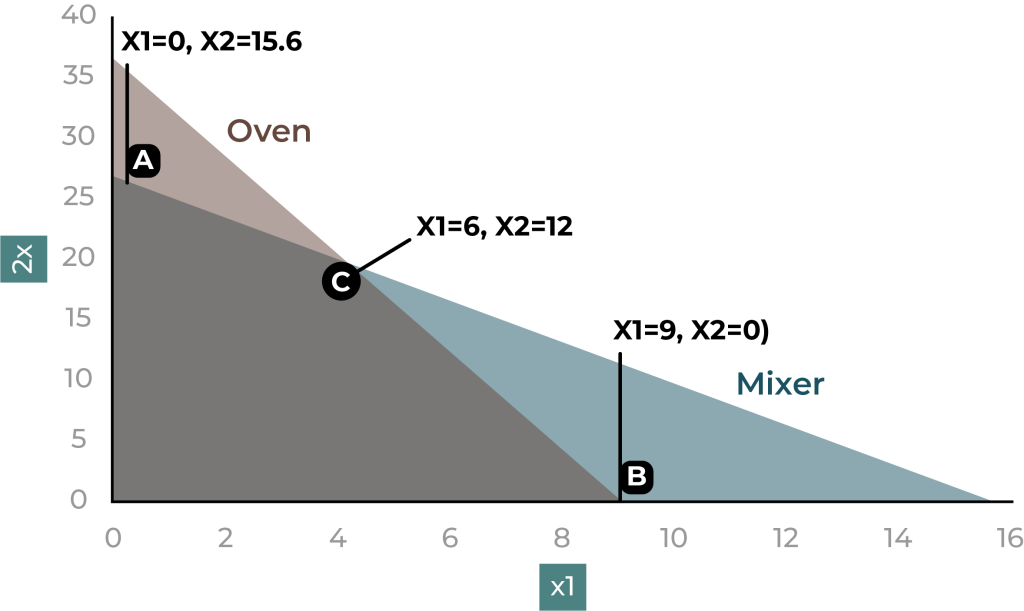
The feasible region contains all combinations of [latex]x_{1}[/latex] (biscuits) and [latex]x_{2}[/latex] (cupcakes) that satisfy the resource constraints. Any point within this region is a potential solution. However, our goal is to maximize the objective function:
[latex]Z = 5x_{1} + 4x_{2}[/latex]
To do this, we evaluate the objective function at the corner points (vertices) of the feasible region. These points represent the optimal candidates due to the convex nature of the feasible region in linear programming.
- Point A: [latex]x_{1} = 0, x_{2} = 15.6[/latex] (maximum cupcakes, no biscuits)
- Point B: [latex]x_{1} = 9, x_{2} = 0[/latex] (maximum biscuits, no cupcakes)
- Point C: Intersection of the two constraint lines (both [latex]x_{1}[/latex] and [latex]x_{2}[/latex] are non-zero)
To find the coordinates of Point C, we solve the system of equations:
[latex]3x_{1} + 5x_{2} = 78[/latex]
[latex]4x_{1} + x_{2} = 36[/latex]
Solving this system yields the exact values of x_{1} and x_{2} at the intersection point, which is likely to provide the optimal solution.
Hint:
[latex]3x_{1}+ 5x_{2} = 78[/latex]
[latex]4x_{1} + 1x_{2}= 36[/latex]
Multiply both sides of the second equation by -5 to eliminate [latex]x_{2}[/latex]
[latex]\begin{align*}3x_{1} + 5x_{2} &= 78\\ 4x_{1} + x_{2} &= 36\\\\ -5(4x_{1} + x_{2}) &= -5(36)\\ -20x_{1} -5x_{2} &= -180\\\\ 3x_{1} + 5x_{2} &= 78\\ -20x_{1} -5x_{2} &= -180\\\\ (3x_{1} + 5x_{2}) + (-20x_{1} -5x_{2}) &= 78 + (-180)\\ -17x_{1} &= -102\\ x_{1} &= 6 \end{align*}[/latex]
Substituting [latex]x_{1}[/latex]value in any of the two equations, we will multiply both sides of the second equation by -5 to eliminate [latex]x_{1}=6[/latex]
Evaluating the Objective Function at Corner Points
Once the coordinates of the corner points (A, B, and C) of the feasible region have been identified, the next step is to evaluate the objective function at each of these points to determine which one yields the maximum profit.
The objective function is:
[latex]Z = 5x_{1} + 4x_{2}[/latex]
We now substitute the values of [latex]x_{1}[/latex] and [latex]x_{2}[/latex] at each point:
At Point A
[latex]\begin{align*}&(x_{1} = 0, x_{2} = 15.6)\\\\ Z &= 5(0) + 4(15.6)\\ &= 62.4 \end{align*}[/latex]
At Point B
[latex]\begin{align*}&(x_{1} = 9, x_{2} = 0)\\\\ Z &= 5(9) + 4(0)\\ &= 45 \end{align*}[/latex]
At Point C
[latex]\begin{align*}&(x_{1} = 6, x_{2} = 12)\\\\ Z &= 5(6) + 4(12)\\ &= 30 + 48\\&= 78 \end{align*}[/latex]
The maximum profit of $78 is achieved at Point C, where Marietta should produce 6 biscuits and 12 cupcakes. This combination makes the most efficient use of her available mixer and oven time while maximizing her special-order profit.

