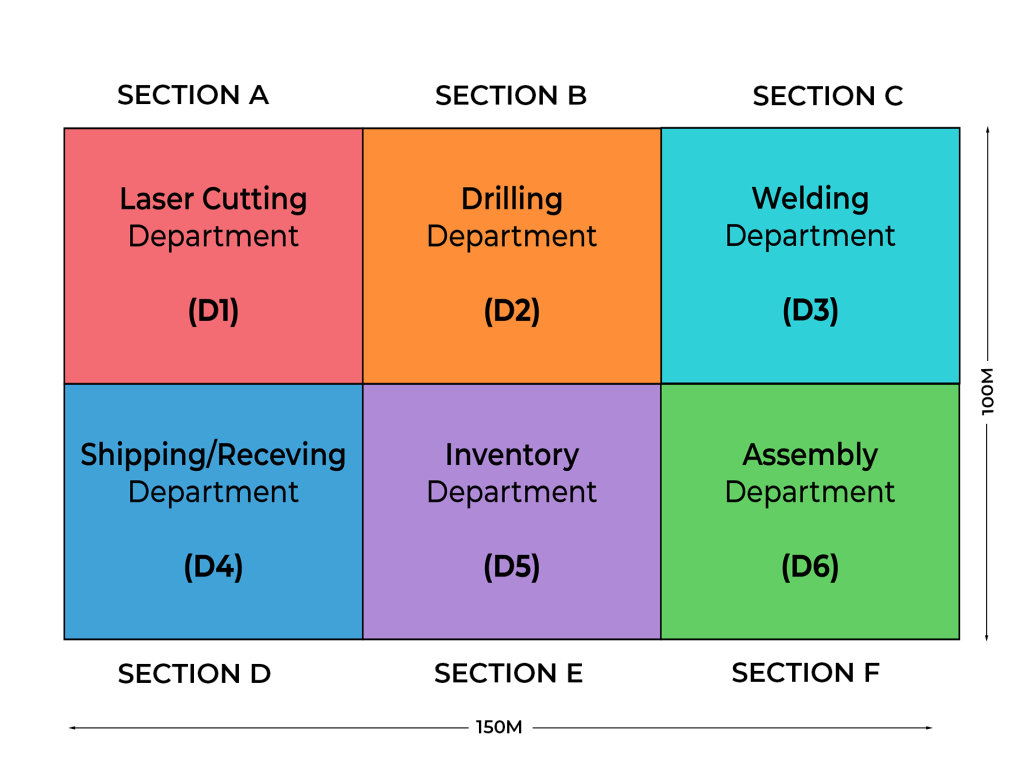
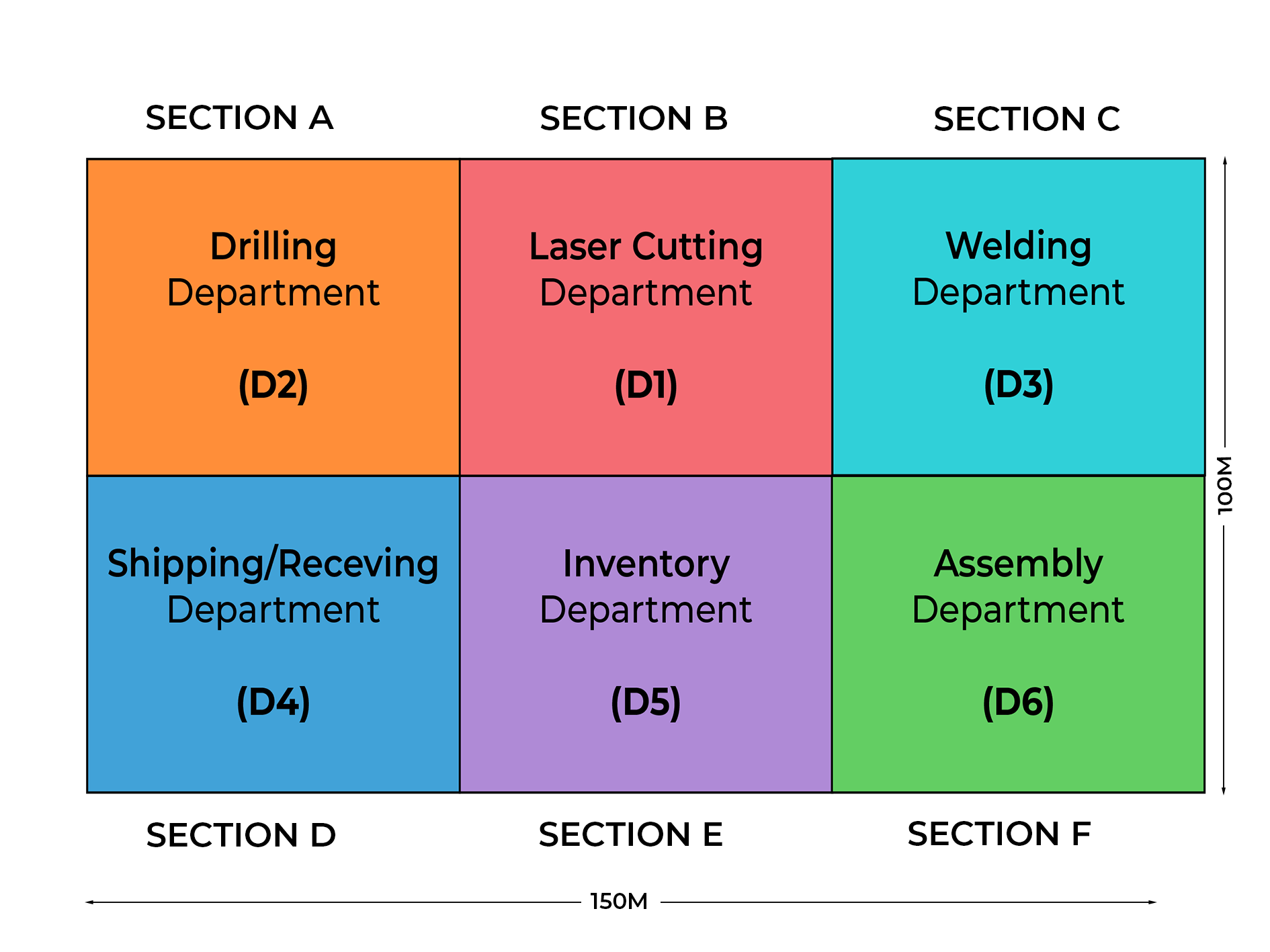
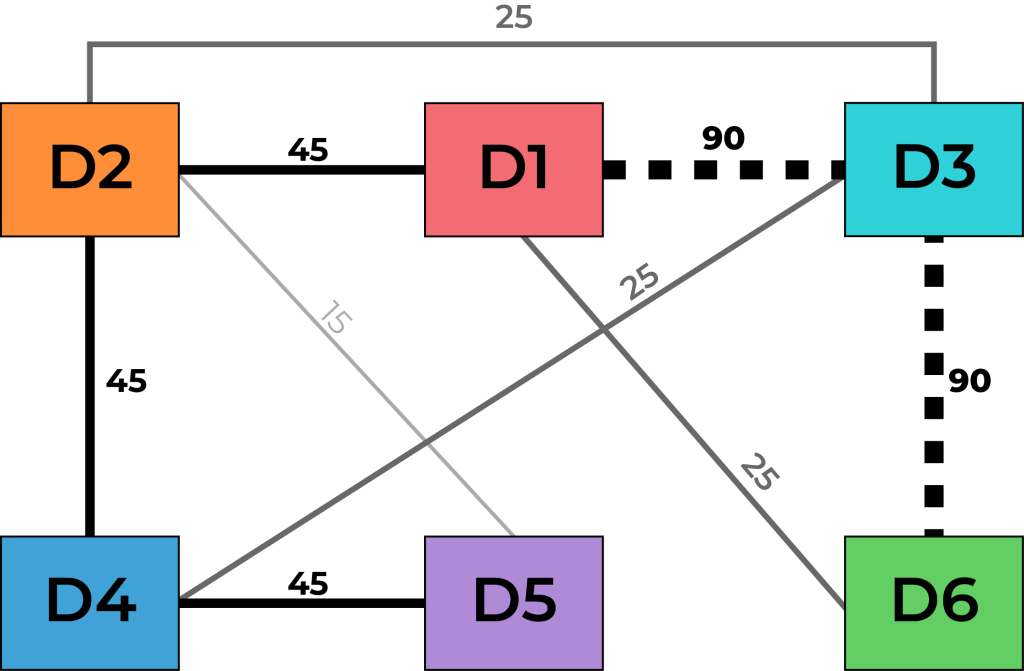
10.7 Material Handling Cost in Process Layout
As discussed earlier, cost-effective material handling and layout flexibility are two key considerations in layout design. These are especially important in process layouts, where general-purpose equipment is used to produce a variety of products or services. In process layouts, materials move between departments based on the specific requirements of each order. To minimize material handling cost, departments should be arranged to reduce both the frequency and distance of moves.
Material handling cost depends on:
- [latex]F[/latex]: Frequency of moves between departments
- [latex]C[/latex]: Cost per move (based on distance or time)
The total material handling cost can be calculated using the formula:
[latex]\text{MH Cost}=\sum_{i=1}^{m}\sum_{j=1}^{m}F_{ij}C_ij[/latex]
- [latex]m[/latex] = # of departments
- [latex]i[/latex], [latex]j[/latex] = individual departments
- [latex]F_{ij}[/latex] = number of loads moved from [latex]i[/latex] to [latex]j[/latex]
- [latex]Cij[/latex] = cost to move a load between [latex]i[/latex] and [latex]j[/latex]
Example Calculation
Consider a factory with six departments producing metal products. The hourly production requires material to move between departments as follows:
- Cost of moving between adjacent departments: $2
- Cost of moving between non-adjacent departments: $4
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 45 | 90 | 0 | 0 | 25 | |
| 2 | 25 | 45 | 15 | 0 | ||
| 3 | 25 | 0 | 90 | |||
| 4 | 45 | 0 | ||||
| 5 | 0 | |||||
| 6 |

Using the formula:
[latex]\begin{align*} \text{MH Cost}&=45(2)+90(4)+25(4)+25(2)+45(2)+15(2)+25(4)+90(2)+45(2) \\ &= \$1,090\text{MH} \end{align*}[/latex]
Reducing Material Handling Cost
To reduce this cost, we can:
- Decrease the frequency of moves (F) – though this may not be feasible without altering the production process.
- Reduce the cost per move (C) – by rearranging departments to shorten travel distances.
For example, relocating departments so that high-traffic pairs (e.g., Departments 1 & 3 and 3 & 6) are adjacent can reduce costs. After rearrangement:
[latex]\begin{align*} \text{New MH Cost}&=45(2)+90(2)+25(2)+25(4)+45(2)+15(2)+25(4)+90(2)+45(2) \\ &= \$910\text{MH} \end{align*}[/latex]
This simple adjustment results in a cost reduction of $180 per hour, demonstrating the impact of thoughtful layout design.
Cell Staffing and Balancing Workload
As discussed earlier, work cells operate as self-contained units, where workers collaborate using shared resources and equipment. To ensure the timely delivery of customer orders, it is essential that each work cell is adequately staffed and that the workload is evenly distributed among team members.
To achieve this, two key factors must be considered:
- Order volume
- Available production time
These factors determine the takt time, also known as the desired cycle time (CTd), which sets the pace of production based on customer demand.
Takt Time Formula
[latex]\begin{align*}\text{Takt Time}(CT_{d}) = \frac{\text{Available Production Time}}{\text{Required Output (Order Volume)}}\end{align*}[/latex]
Takt time represents the maximum amount of time available to produce one unit in order to meet customer expectations.
[latex]\begin{align*}\text{\# of workers needed}=\frac{\sum\;\text{Task times}\;\left(CT_{a}\right)}{\text{Takt time}}\end{align*}[/latex]
Example
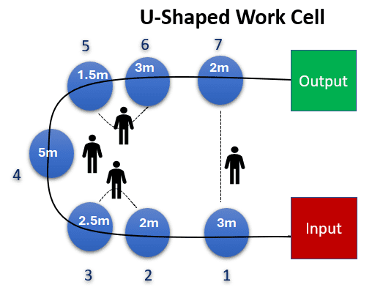
Consider a work cell with seven tasks required to produce a product. The facility operates 8 hours per day, and the customer requires 8 dozen (96 units) of the product daily.
- Available time = 8 hours × 60 minutes = 480 minutes
- Takt time = 480 minutes ÷ 96 units = 5 minutes per unit
This means the cell must produce one unit every 5 minutes to meet demand.
However, the total time required to complete all seven tasks for one unit is 19 minutes. To meet the takt time of 5 minutes, the work must be divided among multiple workers.
[latex]\small\begin{align*}\text{\# of workers needed}&=\frac{\sum\;\text{Task times}\;\left(CT_{a}\right)}{\text{Takt time}}\\[1.5ex]&=\frac{\left(3+2+2.5+5+1.5+3+2\right)}{5}\\[1.5ex]&=3.8\;\text{or}\;4\;\text{workers}\end{align*}[/latex]
Thus, four workers working concurrently in the cell can meet the required output. Each worker would be assigned tasks such that no individual exceeds the 5-minute takt time, ensuring a balanced workload and timely delivery.
Assembly Line Balancing
In product-oriented operations, production tasks are divided among several departments or workstations, each responsible for a specific part of the process. A common example is an assembly line, where fabricated parts or modules are assembled step by step across multiple stations.
However, the time required to complete tasks at each station may vary. This can lead to uneven workloads, where some stations are overburdened while others remain underutilized. Such imbalances can cause delays, bottlenecks, and reduced efficiency.
To address this, the process of line balancing is used. The goal is to distribute tasks across workstations so that each station operates in sync with the desired output rate, also known as the takt time or desired cycle time (CTd).
Takt Time Formula
[latex]\begin{align*}\text{Takt Time}\;\left(CT_{d}\right)=\frac{\text{Available Time for Production}}{\text{Required output (order Volume)}}\end{align*}[/latex]
This value sets the pace of production and helps determine how many workstations are needed to meet demand.
Example
A company is assembling a small suspension system at Meritor Metal. What is the minimum number of stations needed to produce 32 suspension systems in an 8-hour shift?
The total task time required to produce one unit is 68 minutes. The facility operates for 8 hours per day, and the customer requires 32 units daily.
- Available time = (8hrs)(60) = 480 minutes
- Takt time = 480 minutes ÷ 32 units = 15 minutes per unit
- Minimum number of stations = 68 minutes ÷ 15 minutes = 4.53, rounded up to 5 stations
This means the tasks must be distributed across five stations to meet the required output, as shown below:
Evaluating Line Balancing Efficiency
Once the number of stations is determined, it’s important to evaluate how efficiently the tasks are distributed. Line balancing efficiency is calculated as:
[latex]\small\begin{align*}\text{Efficiency}=\frac{\text{Total Task Time}}{\text{Number of Stations}}\times\text{Takt Time}\end{align*}[/latex]
Using the example above:
[latex]\small\begin{align*}\text{Efficiency}=\frac{68}{5}\times 15=\frac{68}{75}=0.907\;\text{or}\;90.7\%\end{align*}[/latex]
If more stations than necessary are used, efficiency drops. For instance, using 6 stations instead of 5:
[latex]\small\begin{align*}\text{Efficiency}=\frac{68}{6}\times 15=\frac{68}{90}=0.755\;\text{or}\;75,5\%\end{align*}[/latex]
This drop in efficiency occurs because some stations would have idle time, leading to the underutilization of resources.