[latexpage]
There are two common procedures that are used to draw the line represented by a linear equation. The first one is called the slope-intercept method and involves using the slope and intercept given in the equation.
If the equation is given in the form \(y = mx + b\), then \(m\) gives the rise over run value and the value \(b\) gives the point where the line crosses the \(y\)-axis, also known as the \(y\)-intercept.
Example 1
Given the following equations, identify the slope and the \(y\)-intercept.
- \(\begin{array}{lll} y = 2x - 3\hspace{0.14in} & \text{Slope }(m)=2\hspace{0.1in}&y\text{-intercept } (b)=-3 \end{array}\)
- \(\begin{array}{lll} y = \dfrac{1}{2}x - 1\hspace{0.08in} & \text{Slope }(m)=\dfrac{1}{2}\hspace{0.1in}&y\text{-intercept } (b)=-1 \end{array}\)
- \(\begin{array}{lll} y = -3x + 4 & \text{Slope }(m)=-3 &y\text{-intercept } (b)=4 \end{array}\)
- \(\begin{array}{lll} y = \dfrac{2}{3}x\hspace{0.34in} & \text{Slope }(m)=\dfrac{2}{3}\hspace{0.1in} &y\text{-intercept } (b)=0 \end{array}\)
When graphing a linear equation using the slope-intercept method, start by using the value given for the \(y\)-intercept. After this point is marked, then identify other points using the slope.
This is shown in the following example.
Example 2
Graph the equation \(y = 2x - 3\).
First, place a dot on the \(y\)-intercept, \(y = -3\), which is placed on the coordinate \((0, -3).\)
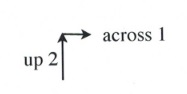
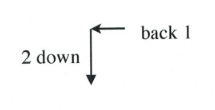
Now, place the next dot using the slope of 2.
A slope of 2 means that the line rises 2 for every 1 across.
Simply, \(m = 2\) is the same as \(m = \dfrac{2}{1}\), where \(\Delta y = 2\) and \(\Delta x = 1\).
Placing these points on the graph becomes a simple counting exercise, which is done as follows:
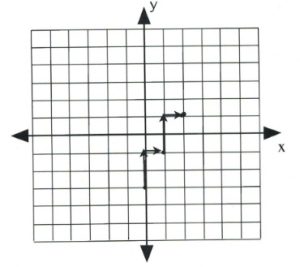
Once several dots have been drawn, draw a line through them, like so:
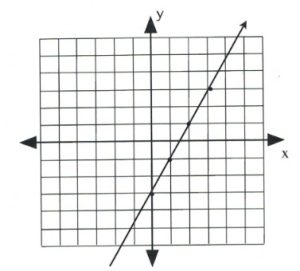
Note that dots can also be drawn in the reverse of what has been drawn here.
Slope is 2 when rise over run is \(\dfrac{2}{1}\) or \(\dfrac{-2}{-1}\), which would be drawn as follows:
Example 3
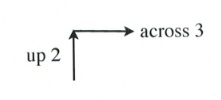
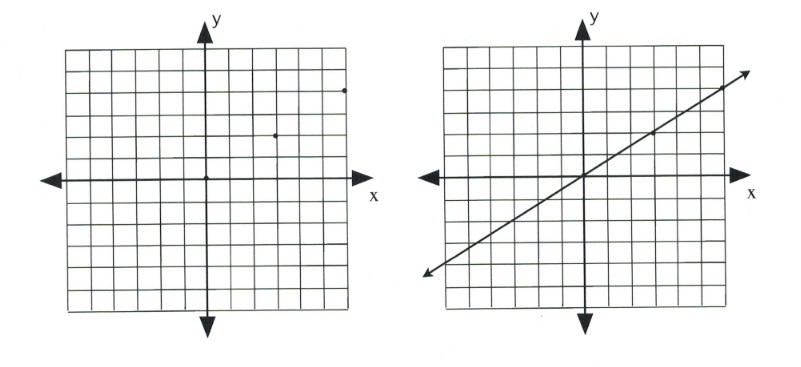
Graph the equation \(y = \dfrac{2}{3}x\).
First, place a dot on the \(y\)-intercept, \((0, 0)\).
Now, place the dots according to the slope, \(\dfrac{2}{3}\).
This will generate the following set of dots on the graph. All that remains is to draw a line through the dots.
The second method of drawing lines represented by linear equations and functions is to identify the two intercepts of the linear equation. Specifically, find \(x\) when \(y = 0\) and find \(y\) when \(x = 0\).
Example 4
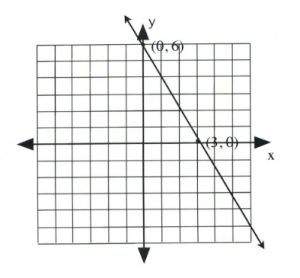
Graph the equation \(2x + y = 6\).
To find the first coordinate, choose \(x = 0\).
This yields:
\[\begin{array}{lllll}
2(0)&+&y&=&6 \\
&&y&=&6
\end{array}\]
Coordinate is \((0, 6)\).
Now choose \(y = 0\).
This yields:
\[\begin{array}{llrll}
2x&+&0&=&6 \\
&&2x&=&6 \\
&&x&=&\frac{6}{2} \text{ or } 3
\end{array}\]
Coordinate is \((3, 0)\).
Draw these coordinates on the graph and draw a line through them.
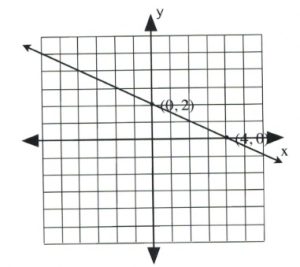
Example 5
Graph the equation \(x + 2y = 4\).
To find the first coordinate, choose \(x = 0\).
This yields:
\[\begin{array}{llrll}
(0)&+&2y&=&4 \\
&&y&=&\frac{4}{2} \text{ or } 2
\end{array}\]
Coordinate is \((0, 2)\).
Now choose \(y = 0\).
This yields:
\[\begin{array}{llrll}
x&+&2(0)&=&4 \\
&&x&=&4
\end{array}\]
Coordinate is \((4, 0)\).
Draw these coordinates on the graph and draw a line through them.
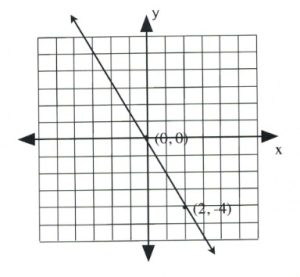
Example 6
Graph the equation \(2x + y = 0\).
To find the first coordinate, choose \(x = 0\).
This yields:
\[\begin{array}{llrll}
2(0)&+&y&=&0 \\
&&y&=&0
\end{array}\]
Coordinate is \((0, 0)\).
Since the intercept is \((0, 0)\), finding the other intercept yields the same coordinate. In this case, choose any value of convenience.
Choose \(x = 2\).
This yields:
\[\begin{array}{rlrlr}
2(2)&+&y&=&0 \\
4&+&y&=&0 \\
-4&&&&-4 \\
\midrule
&&y&=&-4
\end{array}\]
Coordinate is \((2, -4)\).
Draw these coordinates on the graph and draw a line through them.
Questions
For questions 1 to 10, sketch each linear equation using the slope-intercept method.
- \(y = -\dfrac{1}{4}x - 3\)
- \(y = \dfrac{3}{2}x - 1\)
- \(y = -\dfrac{5}{4}x - 4\)
- \(y = -\dfrac{3}{5}x + 1\)
- \(y = -\dfrac{4}{3}x + 2\)
- \(y = \dfrac{5}{3}x + 4\)
- \(y = \dfrac{3}{2}x - 5\)
- \(y = -\dfrac{2}{3}x - 2\)
- \(y = -\dfrac{4}{5}x - 3\)
- \(y = \dfrac{1}{2}x\)
For questions 11 to 20, sketch each linear equation using the \(x\text{-}\) and \(y\)-intercepts.
- \(x + 4y = -4\)
- \(2x - y = 2\)
- \(2x + y = 4\)
- \(3x + 4y = 12\)
- \(2x - y = 2\)
- \(4x + 3y = -12\)
- \(x + y = -5\)
- \(3x + 2y = 6\)
- \(x - y = -2\)
- \(4x - y = -4\)
For questions 21 to 28, sketch each linear equation using any method.
- \(y = -\dfrac{1}{2}x + 3\)
- \(y = 2x - 1\)
- \(y = -\dfrac{5}{4}x\)
- \(y = -3x + 2\)
- \(y = -\dfrac{3}{2}x + 1\)
- \(y = \dfrac{1}{3}x - 3\)
- \(y = \dfrac{3}{2}x + 2\)
- \(y = 2x - 2\)
For questions 29 to 40, reduce and sketch each linear equation using any method.
- \(y + 3 = -\dfrac{4}{5}x + 3\)
- \(y - 4 = \dfrac{1}{2}x\)
- \(x + 5y = -3 + 2y\)
- \(3x - y = 4 + x - 2y\)
- \(4x + 3y = 5 (x + y)\)
- \(3x + 4y = 12 - 2y\)
- \(2x - y = 2 - y \text{ (tricky)}\)
- \(7x + 3y = 2(2x + 2y) + 6\)
- \(x + y = -2x + 3\)
- \(3x + 4y = 3y + 6\)
- \(2(x + y) = -3(x + y) + 5\)
- \(9x - y = 4x + 5\)
Answers to odd questions.
1. \(m=2\)
3. \(m=4\)
5. \(\begin{array}{rrrrlrrr}
\\ \\ \\ \\
x&-&y&=&4&&& \\
-x&&&&-x&&& \\
\midrule
&&(-y&=&-x&+&4)&(-1) \\
&&y&=&x&-&4& \\
&&m&=&1&&&
\end{array}\)
7. \(\begin{array}{rrlrrr}
\\ \\ \\ \\ \\
y&=&\dfrac{1}{3}x&&& \\ \\
\therefore m&=&\dfrac{1}{3} &&& \\
m_{\perp} &=&-1&\div &\dfrac{1}{3}&\text{or} \\
m_{\perp}&=&-3 &&&
\end{array}\)
9. \(\begin{array}{lrlrrrr}
\\ \\ \\ \\
m&=&-\dfrac{1}{3} &&&& \\
m_{\perp} &=&-1&\div &-\dfrac{1}{3}&&\\ \\
m_{\perp}&=&-1 &\cdot &-\dfrac{3}{1}&=& 3
\end{array}\)
11. \(\begin{array}{rrrrlrr}
\\ \\ \\ \\ \\ \\ \\ \\
x&-&3y&=&-6& \\
-x&&&&-x&& \\
\midrule
&&\dfrac{-3y}{-3}&=&\dfrac{-x}{-3}&-&\dfrac{6}{-3} \\ \\
&&y&=&\dfrac{1}{3}x&+&2 \\
&&m_{\perp}&=&-1&\div &\dfrac{1}{3} \\
&&m_{\perp}&=&-3&&
\end{array}\)
13. \(\begin{array}{rrrrlrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
m&=&\dfrac{2}{5}&&&& \\ \\
y&-&y_1&=&m(x&-&x_1) \\
y&-&4&=&\dfrac{2}{5}(x&-&1) \\ \\
y&-&4&=&\dfrac{2}{5}x&-&\dfrac{2}{5} \\ \\
&+&4&&&+&4 \\
\midrule
&&y&=&\dfrac{2}{5}x&+&\dfrac{18}{5}
\end{array}\)
15. \(\begin{array}{rrrrlrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
m&=&\dfrac{1}{2}&&&& \\ \\
y&-&y_1&=&m(x&-&x_1) \\
y&-&4&=&\dfrac{1}{2}(x&-&3) \\ \\
y&-&4&=&\dfrac{1}{2}x&-&\dfrac{3}{2} \\ \\
&+&4&&&+&4 \\
\midrule
&&y&=&\dfrac{1}{2}x&+&\dfrac{5}{2}
\end{array}\)
17. \(\begin{array}{rrrrlrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
m&=&-\dfrac{3}{5}&&&& \\ \\
y&-&y_1&=&m(x&-&x_1) \\
y&-&3&=&-\dfrac{3}{5}(x&-&2) \\ \\
y&-&3&=&-\dfrac{3}{5}x&+&\dfrac{6}{5} \\ \\
&+&3&&&+&3 \\
\midrule
&&y&=&-\dfrac{3}{5}x&+&\dfrac{21}{5}
\end{array}\)
19. \(\begin{array}{rrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
-x&+&y&=&1&&&& \\
+x&&&&+x&&&& \\
\midrule
&&y&=&x&+&1&& \\
&&\therefore m&=&1&&&& \\ \\
y&-&y_1&=&m(x&-&x_1)&& \\
y&-&-5&=&1(x&-&1)&& \\
y&+&5&=&x&-&1&& \\
-y&-&5&&-y&-&5&& \\
\midrule
&&0&=&x&-&y&-&6
\end{array}\)
21. \(\begin{array}{rrrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\
5x&+&y&=&-3&&&&& \\
-5x&&&&-5x&&&&& \\
\midrule
&&y&=&-5x&-&3&&& \\
&&\therefore m&=&-5&&&&& \\ \\
y&-&y_1&=&m(x&-&x_1)&&& \\
y&-&2&=&-5(x&-&5)&&& \\
y&-&2&=&-5x&+&25&&& \\
-y&+&2&&-y&+&2&&& \\
\midrule
&&(0&=&-5x&-&y&+&27)&(-1) \\
&&0&=&5x&+&y&-&27&
\end{array}\)
23. \(\begin{array}{rrrrrrrrr}
\\ \\ \\ \\ \\ \\ \\ \\ \\ \\
-4x&+&y&=&0&&&& \\
+4x&&&&+4x&&&& \\
\midrule
&&y&=&4x&&&& \\
&&\therefore m&=&4&&&& \\ \\
y&-&y_1&=&m(x&-&x_1)&& \\
y&-&2&=&4(x&-&4)&& \\
y&-&2&=&4x&-&16&& \\
-y&+&2&&-y&+&2&& \\
\midrule
&&0&=&4x&-&y&-&14
\end{array}\)
25. \(y=-3\)
27.\(x=-3\)
29. \(y=-1\)
31. \(x=-2\)
33. \(y=3\)
35. \(x=5\)

