4 Union, Intersection, and Intervals
Sets. A set is a collection of well defined objects, called elements.
If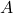 
is a set and 
an element of , we denote 
.
is a set and an element of 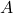, we denote 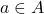.If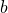 
is not an element of , we denote 
.
is not an element of 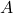, we denote 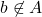. The empty set, denoted,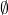 
, doesn’t contain any element.
, doesn’t contain any element.
Subsets. A set is a subset of a set 
if each element of is an element of and we denote 
.
![\[ A\subset B \qquad \Longleftrightarrow \qquad \Big( \forall x\in A \quad \Rightarrow \quad x\in B \Big) \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-991ff0a272fa97366f2f6b2e047b427a_l3.png "Rendered by QuickLaTeX.com")
![\[ \emptyset \subset A \qquad \hbox{ and } \qquad A \subset A \qquad\qquad \hbox{for any set } A\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b3de14b753313373d3c3e2734977d312_l3.png "Rendered by QuickLaTeX.com")
![\[\Big( A \subset B \quad \hbox{ and } \quad B \subset C\quad \Rightarrow A \subset C \Big)\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7dc191a0f4fa086601f40edae9019f29_l3.png "Rendered by QuickLaTeX.com")
Operations on sets
![\[\begin{matrix} A\cup B= \{ x : x\in A \quad \hbox{ or }\quad x\in B\} \qquad \qquad \hbox{ union of } A \hbox{ and } B \\ \\ A\cap B= \{ x : x\in A \quad \hbox{ and } \quad x\in B\} \qquad \qquad \hbox{ intersection of } A \hbox{ and } B\\ \\ A\setminus B= \{ x : x\in A \quad \hbox{ and }\quad x\not\in B\} \qquad \qquad \hbox{ difference of } A \hbox{ and } B \\ \\ A^c= \{ x : x\in U\quad \hbox{ and } \quad x\not\in A\} \qquad \qquad \hbox{ complementary of } A \hbox{ in } U\\ \\ A \times B= \{ (x,y) : x\in A\quad \hbox{ and } \quad y\in B\} \qquad\qquad \hbox{ product of } A \hbox{ and } B \\ \\ \quad A\times A=A^2\end{matrix}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9dc8b6712c0483ae90850672cc881792_l3.png "Rendered by QuickLaTeX.com")
Intervals
![\[\begin{matrix} (a,b)= \{ x : \quad a< x< b\} \qquad \qquad \qquad (a,+\infty)= \{ x :\quad a< x\}\\ \\ [a,b]= \{ x : \quad a \leqslant x\leqslant b\}\qquad \qquad \qquad [a,+\infty)= \{ x : \quad a \leqslant x\} \\ \\ [a,b)= \{ x :\quad a \leqslant x< b\}\qquad \qquad \qquad (-\infty,b)= \{ x : \quad x< b\}\\ \\ (a,b]= \{ x :\quad a<x \leqslant b\} \qquad \qquad \qquad (-\infty,b] = \{ x : \quad x \leqslant b\}\\ \\ (-\infty,+\infty)= \mathbb{R}\qquad \qquad \hbox{ set of all real numbers } \end{matrix} \]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-81ea37989f26aa648f26ce9b31d64b89_l3.png "Rendered by QuickLaTeX.com")
Exercise 1
Exercise 2
Exercise 3
Exercise 4
Exercise 5
