8 Multiplication of Polynomials
Multiplication. The product of two polynomials is obtained by using the distributive property and the law of exponents: ![]() .
.
Some product forms.
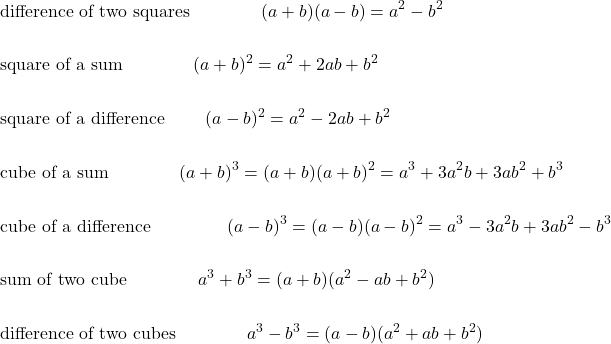
Exercise 1
Show/Hide Solution.
![]()
![]()
![]()
![]() .
.
Exercise 2
Show/Hide Solution.
![]()
![]()
![]() .
.
Exercise 3
Show/Hide Solution.
![]()
![]()
![]()
![]() .
.
Exercise 4
Show/Hide Solution.
![]()
![]()
![]()
![]()
![]() .
.
Exercise 5
Show/Hide Solution.
![]()
![]()
![]() .
.
Exercise 6
Show/Hide Solution.
![]()
![]()
![]() .
.

