24 Lines
![]()
![]()
![]() Two non vertical lines are parallel “// ” if and only if they have the same slope.
Two non vertical lines are parallel “// ” if and only if they have the same slope.
![]() Two non vertical lines are perpendicular ”
Two non vertical lines are perpendicular ” ![]() ” if and only if their slope are negative reciprocals.
” if and only if their slope are negative reciprocals.
If ![]() then
then
![]()
![]()
![]() A horizontal line (slope 0) is perpendicular to a vertical line (no slope)
A horizontal line (slope 0) is perpendicular to a vertical line (no slope)
Exercise 1
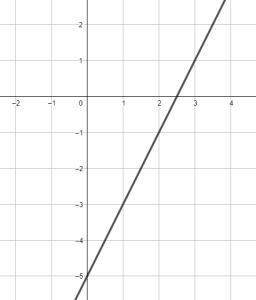
Show/Hide Solution.
The line passes through the points ![]() and
and ![]() .
.
The general equation of this line is in the form : ![]()
For ![]() , we have
, we have ![]() .
.
For ![]() , we obtain
, we obtain ![]() .
.
Thus ![]() and
and ![]() .
.
The equation of the line is : ![]() .
.
Exercise 2
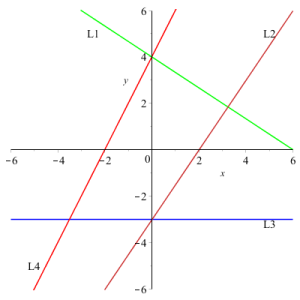
Show/Hide Solution.
Line ![]() passes through the points
passes through the points ![]() and
and ![]() . Thus its equation is
. Thus its equation is ![]() .
.
Line ![]() is horizontal and passes through the points
is horizontal and passes through the points ![]() . Thus its slope is zero and its equation is :
. Thus its slope is zero and its equation is : ![]()
Line ![]() passes through the points
passes through the points ![]() and
and ![]() . Thus its equation is
. Thus its equation is ![]() .
.
Finally, the equation of line ![]() is :
is : ![]() .
.
Exercise 3
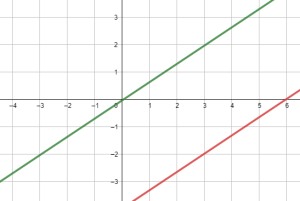
Show/Hide Solution.
The equation of the line that passes through the points ![]() and
and ![]() is given by
is given by
![]()
The equation of the line that passes through the points ![]() and
and ![]() is given by
is given by
![]()
The two lines are parallel since they have the same slope ![]() .
.
Exercise 4
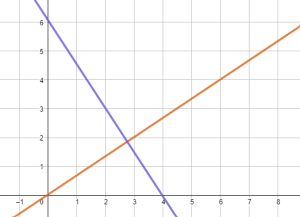
Show/Hide Solution.
The equation of the line that passes through the points ![]() and
and ![]() is given by
is given by
![]()
The equation of the line that passes through the points ![]() and
and ![]() is given by
is given by
![]()
The two lines are perpendicular since their slopes are negative reciprocals : ![]() .
.

