29 Graphs
Plane curve: is the graph of an equation in two variables; that is the set of all points ![]() that satisfy the equation.
that satisfy the equation.
In particular, the graph of a function ![]() is the set
is the set
![]()
![]() -Intercepts =
-Intercepts = ![]() -coordinates of a point where the graph crosses the
-coordinates of a point where the graph crosses the ![]() -axis.
-axis.
![]() -Intercepts =
-Intercepts = ![]() -coordinates of a point where the graph crosses the
-coordinates of a point where the graph crosses the ![]() -axis.
-axis.
Symmetry : a graph ![]() is
is
![]() symmetric with respect to the
symmetric with respect to the ![]() -axis if :
-axis if : ![]()
![]() symmetric with respect to the
symmetric with respect to the ![]() -axis if :
-axis if : ![]()
![]() symmetric with respect to the origin if :
symmetric with respect to the origin if : ![]()
![]() symmetric with respect to the line
symmetric with respect to the line ![]() if :
if : ![]()
Exercise 1

Show/Hide Solution.
Figure A is the graph of a function because the vertical line rule is satisfied.
Figure B is not the graph of a function because the vertical line rule is not satisfied.
Figure C is the graph of a function because the vertical line rule is satisfied.
Figure D cannot be the graph of a function because the vertical line 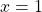 intersects the curve into two different points
intersects the curve into two different points 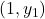 and
and 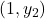 .
.
Figure E is the graph of a function because the vertical line rule is satisfied.
Figure F is not the graph of a function because the vertical line rule is not satisfied.
Exercise 2
Show/Hide Solution.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() are the
are the ![]() -intercepts.
-intercepts.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() are the
are the ![]() -intercepts.
-intercepts.
Exercise 3
Show/Hide Solution.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() are the
are the ![]() -intercepts.
-intercepts.
Set ![]() , then
, then ![]() . Hence
. Hence ![]() is the
is the ![]() -intercept.
-intercept.
Exercise 4
Show/Hide Solution.
* Substitute ![]() for
for ![]() :
: ![]() .
.
Since the equation is unchanged, the graph has ![]() -axis symmetry.
-axis symmetry.
* Substitute ![]() for
for ![]() :
: ![]() .
.
Since the equation is unchanged, the graph has ![]() -axis symmetry.
-axis symmetry.
* Substitute ![]() for
for ![]() and
and ![]() for
for ![]() :
: ![]() .
.
Since the equation is unchanged, the graph has origin symmetry.
Exercise 5
Show/Hide Solution.
* Substitute ![]() for
for ![]() :
: ![]() .
.
Since the equation is changed, the graph does not have ![]() -axis symmetry.
-axis symmetry.
* Substitute ![]() for
for ![]() :
: ![]() .
.
Since the equation is changed, the graph does not have ![]() -axis symmetry.
-axis symmetry.
* Substitute ![]() for
for ![]() and
and ![]() for
for ![]() :
: ![]() .
.
Since the equation is changed, the graph does not have origin symmetry.

