7 Addition and Subtraction of Polynomials

Addition. The sum of polynomials is obtained by adding terms with the same variables raised to the same exponents.

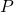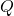Substraction. The difference of two polynomials $P$ and $Q$ is obtained by using the definition : $P- Q= P + (-Q)$ .

Watch a Video

View on YouTube

Show Examples

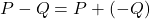Exercise 1

Show/Hide Solution.

$P= 3 x^2 - 5 x - \Big( 5x + 8 - (8- 5 x^2 + (3 x^2 - x + 1) ) \Big)$

$\quad = 3 x^2 - 5 x - \Big( 5x + 8 -8 +5 x^2 - 3 x^2 + x - 1 \Big)$

$\quad = 3 x^2 - 5 x - 5x - 2 x^2 - x + 1$

$\quad = x^2 - 11 x + 1$ .

Exercise 2

Show/Hide Solution.

$A- B= x^2 - 6 x + 10 - ( 3 x^3 - 7 x^2 + x + 1 )$

$\qquad = x^2 - 6 x + 10 - 3 x^3 + 7 x^2 - x - 1$

$\qquad = - 3 x^3 + 8 x^2 - 7 x + 9$ .

$A + B= x^2 - 6 x + 10 + \Big( 3 x^3 - 7 x^2 + x + 1\Big)$

$\qquad = x^2 - 6 x + 10 + 3 x^3 - 7 x^2 + x + 1$

$\qquad = 3 x^3 - 6 x^2 -5 x + 11$ .

Exercise 3

Show/Hide Solution.

$P= 2( 2-5 x) + x^2 (x-1) - (x^4 -1)$

$\qquad = 4-10 x + x^3 - x^2 - x^4 +1$

$\qquad = 5-10 x - x^2 + x^3 - x^4$ .

Exercise 4

Show/Hide Solution.

We have

$(3x-5) -(3)(2x -1) - (2)(- 2x - 2)$

$\quad = (3 - (3)(2) + (2)(2)) x - 5 + (2)(2) + (3)(1)$

$\quad = (1) x + (2)$ .

Exercise 5

Show/Hide Solution.

$(- 3)(5x - 1) - (4)(7x -2)$

$\quad = ((-3)(5) -(4)(7))x + (4)(2) - (-3)(1)$

$\quad = - 43 x + (11)$ .

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Guide to Precalculus Review Copyright © 2025 by Samia CHALLAL is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book