23 Coordinates and Distance
- Let
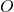 be a fixed point in the plan, called the origin.
be a fixed point in the plan, called the origin.
- Two perpendicular lines passing through
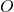 are called the coordinate axes and labelled
are called the coordinate axes and labelled  -axis, and
-axis, and 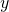 -axis.
-axis.
- The axes divide the plan into 4 parts, called 1st, 2nd, 3rd, and 4th quadrants.
- A point
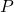 of the plan is represented by the ordered couple
of the plan is represented by the ordered couple 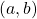 of real numbers
of real numbers  and
and 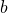 , called coordinates of
, called coordinates of 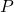 .
.  is the
is the  -coordinate,
-coordinate, 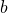 is the
is the 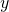 -coordinate.
-coordinate.
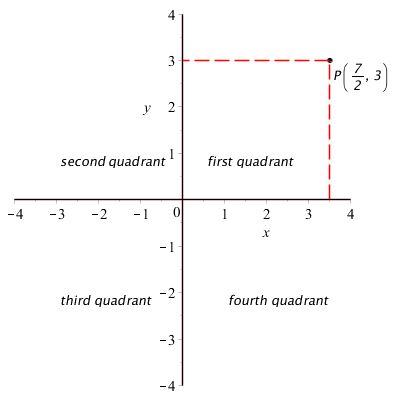
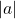 is the distance of
is the distance of 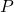 to the
to the 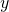 -axis,
-axis,  is the distance of
is the distance of 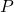 to the
to the  -axis.
-axis.
- The distance between two points
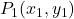 and
and 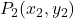 is given by:
is given by: 
- The coordinates of the the midpoint of a line segment joining
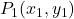 and
and 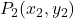 is given by:
is given by:
![Rendered by QuickLaTeX.com \[\displaystyle{\Big( \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\Big)}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-05d4da14eab01e89c0379c0f37a7a48d_l3.png)
Exercise 1
Exercise 2
Show/Hide Solution.
The coordinates of the midpoint of the segment that joins the two points ![]() and
and ![]() are
are
![]()
Exercise 3
Show/Hide Solution.
The length of the sides of the triangle are:
![]()
![]()
![]() .
.
We have ![]() . Thus, by the Pythagorean theorem, the triangle is a right triangle at
. Thus, by the Pythagorean theorem, the triangle is a right triangle at ![]() .
.
Exercise 4
Show/Hide Solution.
The distance between the point ![]() and the origin is given by
and the origin is given by
![]() .
.
The distance between the point ![]() and the origin is given by
and the origin is given by
![]() .
.
Thus the points ![]() and
and ![]() are at the same distance from the origin.
are at the same distance from the origin.
Exercise 5
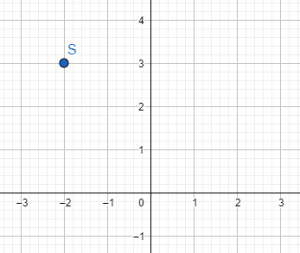
Show/Hide Solution.
The distance between the point ![]() and the
and the ![]() -axis is
-axis is
![]()
The distance between the point ![]() and the
and the ![]() -axis is
-axis is
![]()

