19 Linear Inequations
![]() A linear inequality is a statement in the form
A linear inequality is a statement in the form ![]() , or
, or ![]() , or
, or ![]() , or
, or ![]() , where
, where ![]() is a variable.
is a variable.
The variable that makes the statement true is called a solution of the equation.
![]() How to solve, for example,
How to solve, for example, ![]() ?
?
![]() combine all variable terms in one side
combine all variable terms in one side
![]() combine all constants terms on the other
combine all constants terms on the other
![]() divide both sides by the coefficient of the
divide both sides by the coefficient of the
variable and change the inequality to ![]() if
if ![]() .
.
![]()
![]()
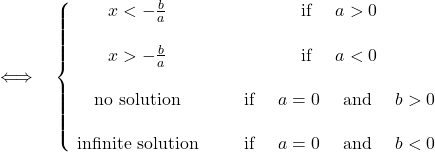
Exercise 1
Show/Hide Solution.
The set of possible solutions is the interval: ![]() .
.
Exercise 2
Show/Hide Solution.
The set of possible solutions is the interval: ![]() .
.
Exercise 3
Show/Hide Solution.
We have
![]()
![]()
![]()
which is true for any ![]() since
since ![]()
![]() .
.
The set of all possible solutions is the interval: ![]() .
.

