Linear Equations

Samia CHALLAL

17 Linear Equations

$\bullet$ A linear equation is a statement in the form $a x + b = 0$ , where $x$ is a variable.

The variable that makes the statement true is called a solution of the equation.

$\bullet$ How to solve $a x + b = 0$ ?

– combine all variable terms in one side

– combine all constants terms on the other

– divide both sides by the coefficient of the variable.

$\bullet$

$a x + b = 0 \,\,\Longleftrightarrow\,\, a x = - b \,\,\Longleftrightarrow \left\{ \begin{matrix} x= - \frac{b}{a} & \hbox { if } \quad a\neq 0 \\ \\ \hbox{ no solution } & \hbox { if } \quad a = 0 \quad \hbox { and } \quad b\neq 0\\ \\ \hbox{ infinite solution } & \hbox { if } \quad a =0 \quad \hbox { and } \quad b= 0 \end{matrix} \right.$

Watch a Video

View on YouTube

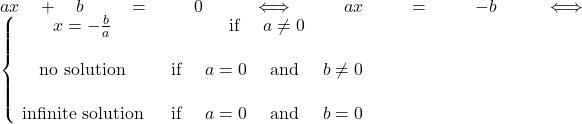
Exercise 1

Show/Hide Solution.

We have

$\displaystyle{ {-2} - 2 [ {-5} - 3 ( {4} - x ) ] = {2} }$

$\displaystyle{\qquad \Leftrightarrow \qquad {-2} - 2 ({-5}) + 6 ({4}) - 6 x = {2} }$

$\displaystyle{\qquad \Leftrightarrow \qquad x= \frac{1}{6 } ({-2}- ({2} )- 2 ({-5}) + 6( {4} )) = \frac{{30}}{6} =5. }$

Exercise 2

Show/Hide Solution.

For $x\not= 0$ , we have

$\displaystyle{\frac{x + 1}{{8}} = \frac{x - 1}{{8}} + \frac{{9}}{x} }$

$\displaystyle{\qquad \Leftrightarrow \qquad \frac{x + 1}{{8}} = \frac{x (x - 1) + ( {8} ) ({9} )}{{9} x} }$

$\qquad \Leftrightarrow \qquad ( {8}) x\Big(x + 1\Big) = {8}\Big(x (x - 1) + ({8} )({9} )\Big)$

$\displaystyle{\qquad \Leftrightarrow \qquad x^2 + x = x^2-x + ( {8} ) ({9} )$

$\qquad \Leftrightarrow \qquad x= \displaystyle{ \frac{{8} ({9})}{2} = \frac{{72}}{2} = 36.}$

Exercise 3

Show/Hide Solution.

For $x\neq \pm 1$ , we have

$\displaystyle{ \frac{{6}}{x-1} + \frac{{4}}{x+1} = \frac{ {4} }{x^2-1} }$

$\displaystyle{ \qquad \Leftrightarrow \qquad \frac{{6} (x+1) + {4} (x-1)}{x^2-1} = \frac{ {4} }{x^2-1} }$

$\displaystyle{\qquad \Leftrightarrow \qquad ({6}+{4}) x + {6}- {4} = {4} }$

$\displaystyle{ \qquad \Leftrightarrow \qquad x= \frac{ {4} + {4} - {6} }{{6}+{4}} = \frac{{2} }{{10}} = \frac{{1} }{{5}} } .$

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

License

Share This Book