14 Simplifying Rational Expressions
* A rational expression
is an expression that can be simplified in the form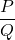 where
where 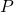 and
and 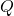 are polynomials.
are polynomials.
is an expression that can be simplified in the form
* To simplify a rational expression, we can:
– combine numerator and denominator into single quotients, then divide : 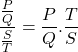
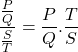
– reduce to the same denominator : 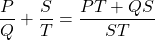
– reduce to lower terms : 
Exercise 1
Show/Hide Solution.
We have
![]()
![]() .
.
Thus, by simplifying the common factor ![]() , we obtain
, we obtain
![]() .
.
Exercise 2
Show/Hide Solution.
We have
![]() =
= ![]() =
= ![]() .
.
Exercise 3
Show/Hide Solution.
We have
![]()
![]()
Thus, by simplifying the common factor ![]() , we obtain
, we obtain
![]() .
.

