Volume
15 Volume d’un cube ou d’un réservoir rectangulaire
Sélectionne le lecteur audio suivant pour écouter en lisant cette section.
 Si l’on vous demandait de décrire le volume d’un objet, que diriez-vous? Comment décririez-vous les unités de votre calcul?
Si l’on vous demandait de décrire le volume d’un objet, que diriez-vous? Comment décririez-vous les unités de votre calcul?
Ce chapitre traite du calcul du volume et des unités utilisées lors du calcul d’un volume.
Dans le chapitre précédent, nous avons abordé le périmètre, qui est une mesure linéaire. Comme nous l’avons constaté, le périmètre est unidimensionnel et présente essentiellement les caractéristiques d’une ligne. Un bon exemple de périmètre serait de faire le tour d’un terrain de soccer. Vous parcouriez le périmètre du terrain.
Nous avons ensuite examiné l’aire, qui est une mesure bidimensionnelle. Un bon exemple : un dessus de table. Si vous deviez prendre un pinceau et repeindre le dessus de la table, vous peindriez l’aire du dessus de la table.

Lorsqu’il s’agit de volume, nous ajoutons une dimension supplémentaire, et le volume devient alors une mesure tridimensionnelle. Un bon exemple d’objet tridimensionnel : la planète Terre.

Voici une autre représentation visuelle des trois. Chaque ligne représente un plan.
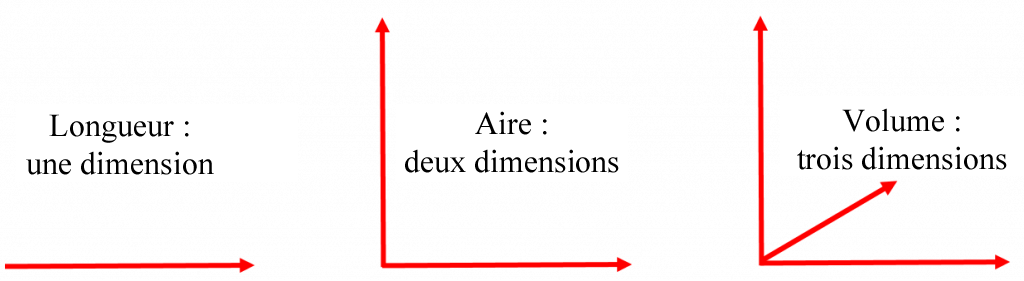
Revenons à présent aux unités. Lorsqu’il s’agit de mesures linéaires, nous traitons les unités telles qu’elles sont. Je veux dire par là que nous obtenons la réponse en mètres, en pieds, en pouces, en centimètres, etc.
Lorsqu’il s’agit de surface, nous continuons à utiliser des unités telles que le mètre, mais elles sont mises au carré pour indiquer qu’elles ont deux dimensions. Par exemple, un appartement peut avoir une aire de 1200 pieds carrés ou 1200 pi². La mise au carré des pieds indique deux dimensions, comme la largeur ET la longueur.
Maintenant, nous ajoutons une dimension supplémentaire au tableau. Non seulement nous avons peut-être une longueur et une largeur, mais nous avons peut-être aussi une profondeur. Ce qui nous amène à nous demander : « Quelles seraient les unités dans cette situation? »
Si nos unité étaient des mètres, la réponse serait des mètres cubes. Pour le formuler comme l’aire, cela ressemblerait à ceci :
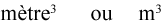
Le « 3 » dans ce cas représente trois dimensions et il donne le sens au terme « cube » lorsque nous le lisons. Nous sommes maintenant prêts à poursuivre et à découvrir la formule du volume d’objets précis.
Le volume d’un cube
Lorsqu’on parle de « cube », on peut penser à un carré, mais avec une dimension de plus. Chaque dimension d’un carré est identique et le cube suit cette même logique.
Si l’on ajoute une troisième dimension, toutes les dimensions possibles sont identiques. Jetez un coup d’œil à l’un des cubes les plus célèbres du monde :

Pour trouver le volume du cube, nous devons multiplier ses trois arêtes. Plus précisément, nous cherchons à multiplier la longueur, la largeur et la hauteur. Comme les trois arêtes sont identiques, la formule se présente comme suit :
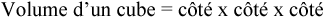
Trouver l’aire d’un cube est assez simple. Il vous suffit de connaître la longueur d’une arête, et vous avez toutes les informations dont vous avez besoin.
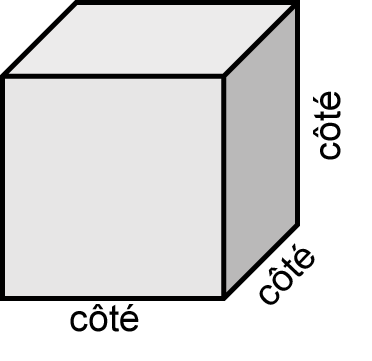
Exemple
Trouvez le volume d’un cube dont l’une des arêtes mesure 7 pouces.
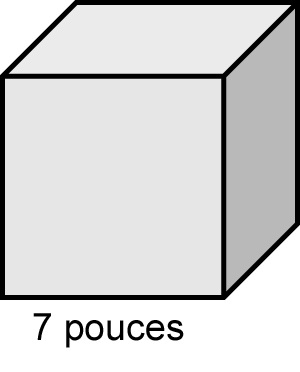
Étape 1 : Écrivez la formule.
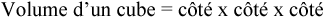
Étape 2 : Trouver le volume.
Comme toutes les arêtes d’un cube sont égales, cela signifie que chaque arête mesure 7 pouces.
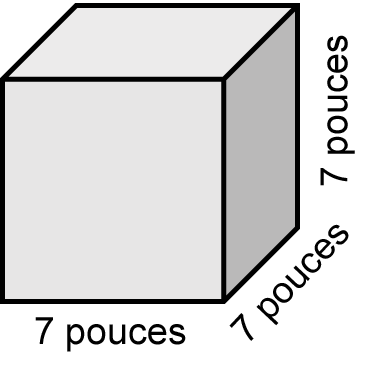
Donc, lorsqu’on met les variables dans l’équation, elles sont toutes égales.
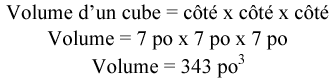
Volume d’un cube ou d’un réservoir rectangulaire
La façon de calculer le volume d’un réservoir rectangulaire est très semblable à la façon de calculer le volume d’un cube, à l’exception du fait que les dimensions d’un réservoir rectangulaire sont toutes différentes. À partir de maintenant, nous parlerons d’un réservoir.
Le nom des variables du réservoir sont différents. Pour le rectangle, nos variables étaient la longueur et la largeur.
Maintenant, nous ajoutons simplement une autre variable que nous appellerons « hauteur ».
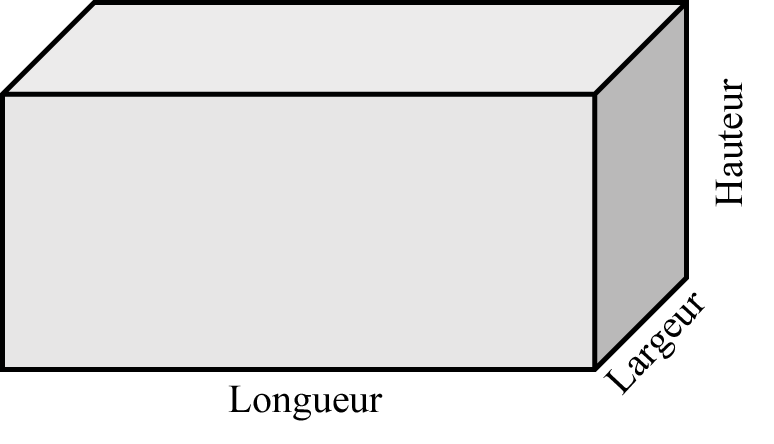
La formule sera similaire à celle d’un cube, mais la variable « arête » sera remplacée par les trois variables du réservoir.
Formule :
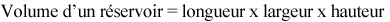
Exemple
Calculez le volume d’un réservoir qui a une longueur de 17 pouces, une largeur de 12 pouces et une hauteur de 13 pouces.
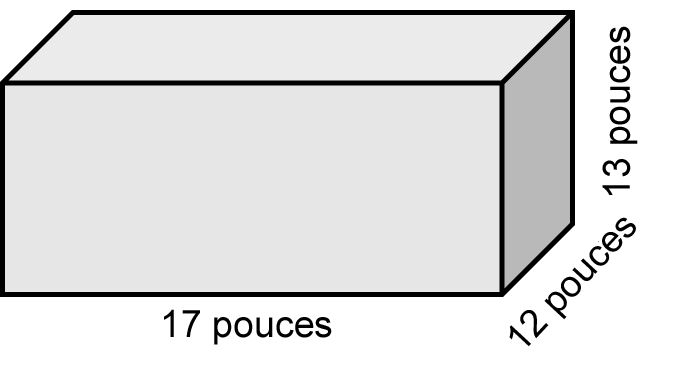
Étape 1 : Écrivez la formule.
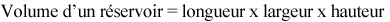
Étape 2 : Trouver le volume.
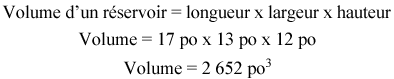

Compliquons les choses maintenant et exprimons la réponse en pieds cubes.
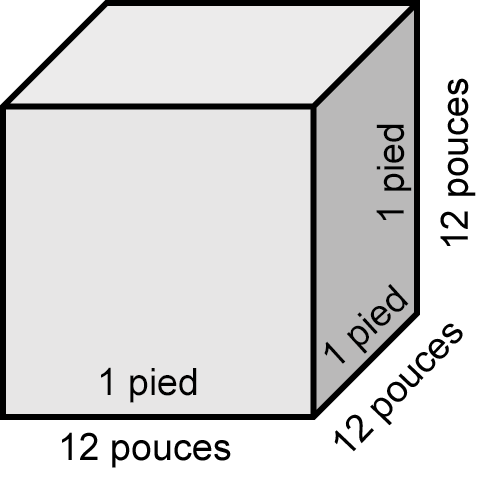
La première chose à faire est de calculer combien de pouces cubes il y a dans un pied cube et la meilleure façon de le faire est de façon visuelle.
Nous sommes tous d’accord pour dire que 1 pied équivaut à 12 pouces. En utilisant la formule d’un cube, nous obtenons ce qui suit :
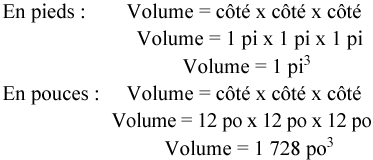
Nous avons donc maintenant :
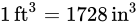
Nous pouvons maintenant répondre à la question.
Combien de pieds cubes y a-t-il dans un réservoir qui contient 2 652 pouces cubes?
Ce que vous faites ici, c’est prendre le nombre de pouces cubes et le diviser par le nombre de pouces cubes qu’il y a dans un pied cube.
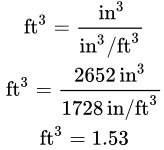
Passons en revue un autre exemple et, encore une fois, compliquons la question.
Exemple
Calcule le volume d’un réservoir qui a une longueur de 22 pouces, une largeur de 14 pouces et une hauteur de 3 080 pouces.
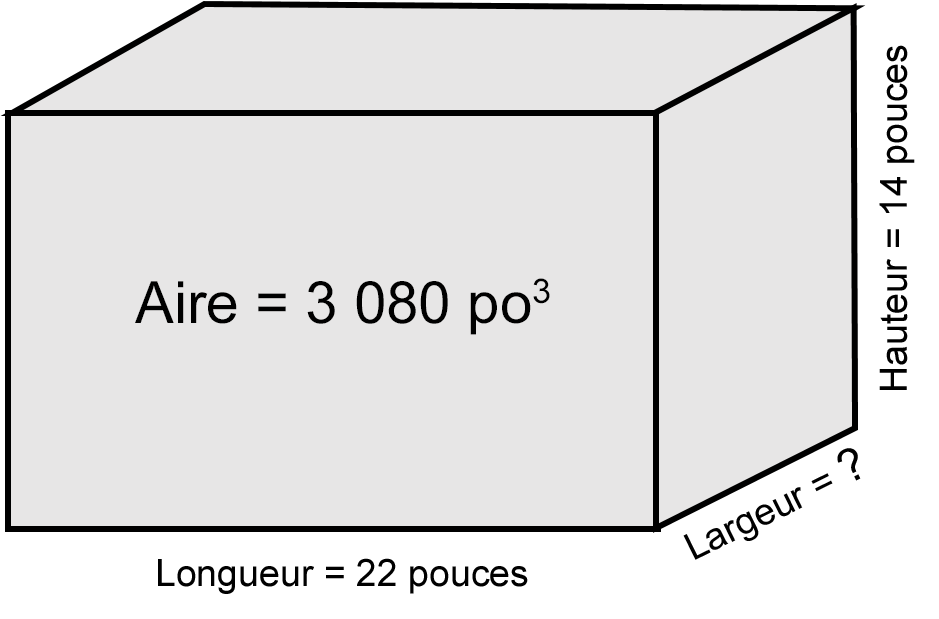
Étape 1 : Écrivez la formule.
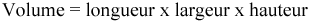
Étape 2 : Réarrange la formule pour trouver la largeur.
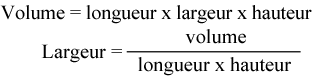
Étape 3 : Calculer la largeur.

Exercices pratiques
Essayez quelques exercices pratiques pour vous-même. Assurez-vous de consulter les réponses vidéo pour voir comment vous vous êtes débrouillé.
Question 1

Lyle travaille pour une entreprise d’installations de gaz qui s’appelle « Night and Day Heating ». Il conçoit un système de chauffage pour un bâtiment conçu par un architecte excentrique. Le bâtiment a la forme d’un cube dont l’un des côtés mesure 30 pieds.
Lyle doit prendre en compte le volume du bâtiment avant de concevoir le système. Quel est le volume du bâtiment en forme de cube?
Question 2

Kate est propriétaire d’une entreprise d’installation de fosses septiques dans une région rurale de la Colombie-Britannique et elle vient d’embaucher Rachael, originaire d’Afrique de l’Est et qui n’a jamais installé de système septique auparavant.
Selon l’ingénieur qui a conçu le système, le réservoir est pour une maison de quatre chambres à coucher et son volume total doit être d’au moins 170 pieds cubes. Les dimensions du réservoir qu’elle prévoit d’installer sont ci-dessous. Compte tenu de ces dimensions, la fosse septique sera-t-elle assez grande pour répondre aux demandes de l’ingénieur?
Longueur = 7,5 pieds
Largeur = 5,25 pieds
Hauteur = 4,5 pieds

