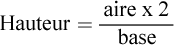Périmètre et aire
13 Aire
Sélectionnez le lecteur audio suivant pour écouter en lisant cette section.

Jean est un peintre qui va peinturer un mur dans une maison. Il a besoin de savoir la quantité de peinture qu’il doit acheter pour ce mur. Il sait que le mur a la forme d’un rectangle et que les dimensions sont : 10 pieds de haut sur 27 pieds de large.
Comment pensez-vous qu’il devrait s’y prendre pour résoudre ce problème?
La réponse se trouve dans la calcul de l’aire du mur. Un pot de peinture peut couvrir une certaine surface et si Jean peut calculer la surface du mur, il pourra calculer le nombre de pots de peinture dont il aura besoin.
La première chose à faire ici est d’écrire la définition de l’aire.
Aire : La quantité d’espace à l’intérieur des limites d’un objet plat (à 2 dimensions) tel qu’un triangle, un carré ou un cercle.
Voici quelques formes bidimensionnelles ombrées en gris. La partie grise représente l’aire de l’objet tandis que les lignes noires entourant l’objet représentent le périmètre.

L’aire d’un carré ou d’un rectangle
Avant de commencer à calculer l’aire d’un carré ou d’un rectangle, revenons rapidement au périmètre et plus précisément sur la façon dont nous avons défini les dimensions d’un carré et d’un rectangle.

Une fois de plus, la partie ombrée en gris correspond à l’aire de chacun des objets. La question est…

Peut-on utiliser ces dimensions pour calculer l’aire? Ou devons-nous trouver d’autres dimensions pour obtenir notre réponse?
Eh bien, il s’avère que ces dimensions nous conviendront. Non seulement elles sont utiles pour calculer le périmètre, mais elles fonctionnent aussi très bien pour calculer l’aire.

La question suivante est alors de savoir COMMENT utiliser ces dimensions?
Avant de passer à la suite pour voir comment on fait, prenez une minute pour y réfléchir. Peut-être même écrire certaines de vos réflexions. Une fois de plus, cela nous ramène à quelque chose dont nous avons déjà parlé. Si vous êtes capable de comprendre le concept, alors le processus implique moins de mémorisation.

Voici les formules pour calculer l’aire d’un carré et d’un rectangle.
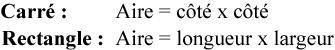

Attention, il y a quelques différences par rapport au périmètre. Tout d’abord, il s’agit d’une multiplication et non plus d’une addition. Cela nous amène à notre deuxième point.
En jetant un coup d’œil à la formule du carré, nous voyons que nous multiplions un côté par un côté. Comme tous les côtés sont identiques, les deux côtés que nous multiplions n’ont pas vraiment d’importance.
Le problème, ce sont les unités avec lesquelles nous nous retrouvons. N’oubliez pas que lorsqu’on parle de périmètre, on a affaire à une ligne unidimensionnelle. Nos unités sont linéaires ou essentiellement unidimensionnelles.
Avec l’aire, nous obtenons des unités qui nous donnent une réponse en utilisant des unités bidimensionnelles. Rien de tel qu’un exemple pour bien comprendre.
Imaginons que nous avons un carré dont chaque côté mesure 5 pouces.

En utilisant la formule de l’aire d’un carré, nous obtenons…
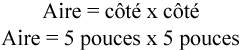
Nous pouvons conclure que 5 fois 5 est égal à 25 mais que se passe-t-il lorsque nous multiplions des pouces par des pouces?
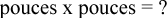
Eh bien, les pouces multipliés par les pouces donnent des pouces au carré ou, si vous deviez l’écrire, cela ressemblerait à ceci :
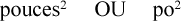
Ainsi, lorsque vous voyez des mesures telles que des pieds, des pouces, des milles, des kilomètres, etc. suivies du symbole du carré, il s’agit d la mesure d’une aire. En d’autres termes, il s’agit d’une mesure exprimée en deux dimensions.
Si nous reprenons notre exemple, nous obtiendrons ceci :
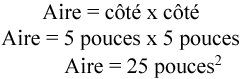
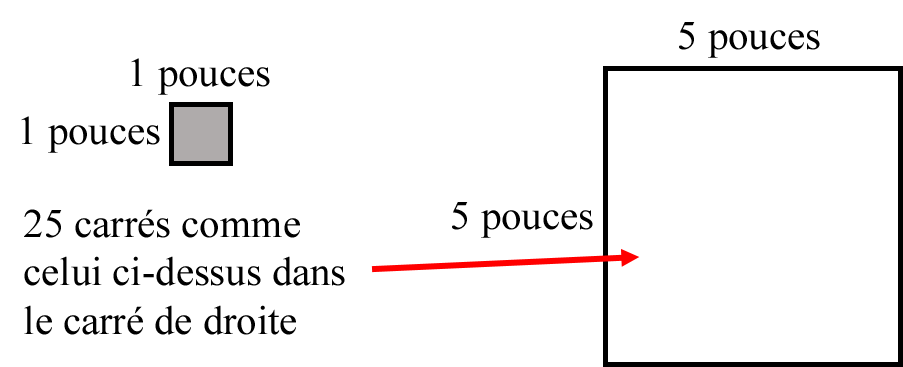
Si nous devions l’examiner visuellement, voici ce que nous aurions:
Exemple
Calculez la surface d’un carré dont le côté mesure 14 cm.
Étape 1 : Écrivez la formule.
Étape 2 : Calculez l’aire.
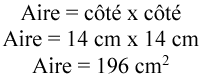
Exemple
Un rectangle a une longueur de 22 pouces et une largeur de 15 pouces. Calculez l’aire du rectangle.
Étape 1 : Écrivez la formule.
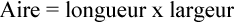
Étape 2 : Calculez l’aire.
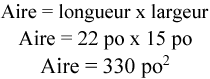

Disons que nous voulons obtenir la réponse en pieds carrés (pi²). Comment pensez-vous procéder? La meilleure façon de voir cela est visuelle. La première chose à retenir, c’est que :
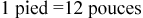
Rappelez-vous qu’il s’agit d’une mesure linéaire ou unidimensionnelle. Ce que nous cherchons à obtenir, c’est une mesure bidimensionnelle.
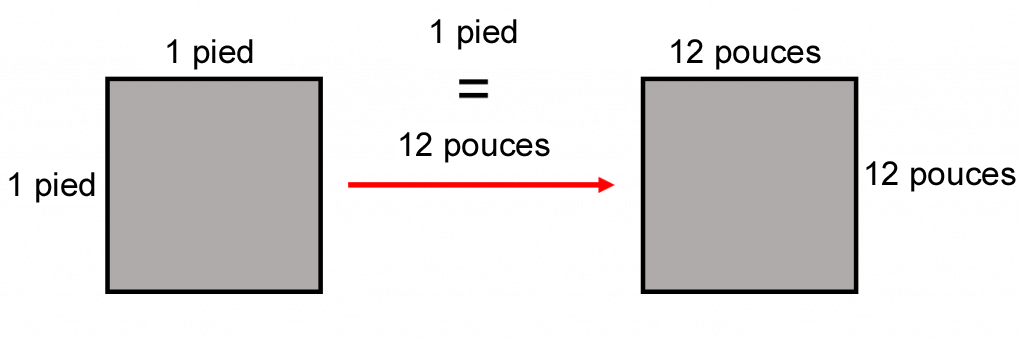

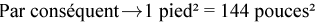
En gros, il faut 144 pouces carrés pour faire un pied carré.
Exemple
Un carré a un côté de 15 pouces. Quelle est l’aire du carré en pieds carrés?
Étape 1 : Écrivez la formule.
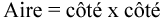
Étape 2 : Calculez l’aire.
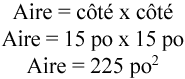
Étape 3 : Convertissez les pouces au carré en pieds au carré.

L’aire d’un triangle

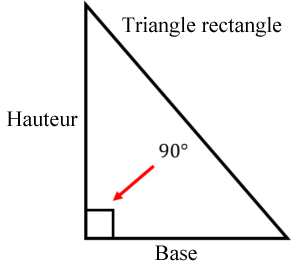
Bien qu’un triangle ait des lignes droites semblables à celles d’un carré ou d’un rectangle, il diffère par le fait qu’il a trois côtés et non quatre. Cela signifie que les équations précédentes utilisant le côté, la longueur ou la largeur ne fonctionneront pas dans cet exemple. Examinez l’image du triangle. Dans notre équation, nous allons travailler avec la « base » et de « hauteur ».
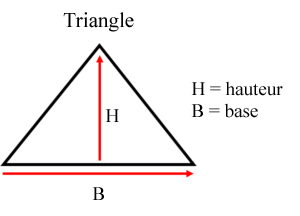
Les triangles ne sont pas toujours disposés comme ici au-dessus. Mais cela n’a pas d’importance car vous pouvez tourner le triangle dans tous les sens et finir par trouver la « base » et la « hauteur ».
Une autre version d’un triangle est illustrée à gauche. Cette version est celle qui nous permet de trouver notre formule pour l’aire d’un triangle. Ce que nous avons à gauche est ce que l’on appelle un triangle « rectangle ». Un triangle rectangle est défini comme tout triangle dont l’un des angles est de 90°. Il possède également les caractéristiques d’un triangle, c’est-à-dire qu’il a une base et une hauteur ainsi que trois côtés. Maintenant, prenez ce triangle et faites-en un autre exactement similaire, mais inversez sa position comme dans l’image ci-dessous.
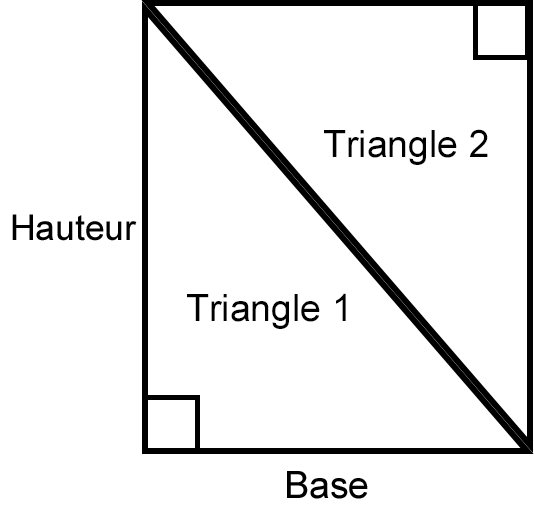
Le dessin ci-dessus montre qu’en réunissant les deux triangles, on obtient un rectangle. Ils pourraient également former un carré si la base et la hauteur étaient identiques.
Quoi qu’il en soit, lorsque nous revenons sur la formule d’un rectangle, il s’agit de la longueur multipliée par la largeur. Dans ce cas, en multipliant la base par la hauteur, nous obtiendrons l’aire des deux triangles.
Il est donc logique que l’aire de l’un des triangles soit l’aire de la base multipliée par la hauteur.
Et finalement, c’est exactement la formule d’un triangle. Notez que cela fonctionne pour n’importe quel triangle, même si ce n’est pas un triangle rectangle. L’objectif principal est d’obtenir la bonne mesure de la base et la bonne mesure de la hauteur.
Formule :

Prenons un exemple.
Exemple
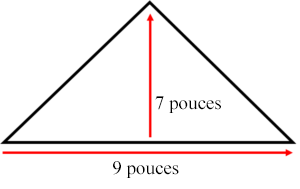
Trouvez la surface d’un triangle dont la base mesure 9 pouces et la hauteur 7 pouces.
Étape 1 : Écrivez la formule.

Étape 2 : Calculez l’aire.

Exemples
Trouvez la surface d’un triangle dont la base mesure 12 pouces et la hauteur 10 pouces.
Étape 1 : Écrivez la formule.

Étape 2 : Calculez l’aire.
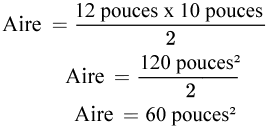
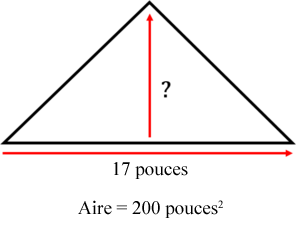
Nous allons essayer un autre exemple, mais cette fois-ci, nous allons changer un peu les choses et l’aire et la base seront données et nous devrons calculer la hauteur.
Exemple

Regardez les unités de la réponse finale. Notez qu’elles sont exprimées en pouces mais que dans la question, l’aire est exprimée en pouces au carré.
Il est logique que la hauteur soit exprimée en pouces puisqu’il s’agit d’une mesure linéaire et unidimensionnelle, mais comment en arrivons-nous à cette réponse? Y a-t-il une explication mathématique à cela?
La réponse est oui. Voici comment ça fonctionne.
Ce dont nous avons besoin pour commencer, ce sont les unités de l’équation avec laquelle nous travaillons. Nous ne nous préoccupons pas des valeurs réelles, mais seulement des unités.

Exercices pratiques
Essayez quelques exercices pratiques pour vous-même. Assurez-vous de consulter les réponses vidéo pour voir comment vous vous êtes débrouillé.
Question 1

Revenons à Jean, le peintre, pour celle-ci. Jean doit peindre un mur dont les dimensions sont de 22 pieds de long sur 9 pieds de large. La largeur correspond en fait à la hauteur du mur dans ce cas-ci. Calculez l’aire en pieds carrés et en pouces carrés.
Question 2

Restons avec Jean le peintre pour la deuxième question. On lui a demandé de mettre une nouvelle couche de peinture sur une grange. Il a calculé l’aire de la majeure partie de la grange en utilisant la formule pour un rectangle, mais la partie supérieure de la grange forme un triangle. Calcule l’aire à peindre dans la partie triangulaire de la grange en gardant à l’esprit qu’il y a un triangle à une extrémité de la grange et un autre triangle à l’autre extrémité. La partie triangulaire a une base de 37 pieds et une hauteur de 9 pieds.
Aire d’un cercle

Si vous vous souvenez bien, dans la partie de ce chapitre consacrée au périmètre, nous avons étudié le périmètre (la circonférence) d’un cercle. Pour obtenir ce calcul, nous devions connaître l’une des deux caractéristiques du cercle. Pour trouver l’aire d’un cercle c’est pareil. La hauteur, la largeur ou la longueur ne fonctionneront pas pour nous, car il n’y a pas de lignes droites dans un cercle. Ce qu’il nous faut pour travailler, c’est le rayon ou le diamètre.
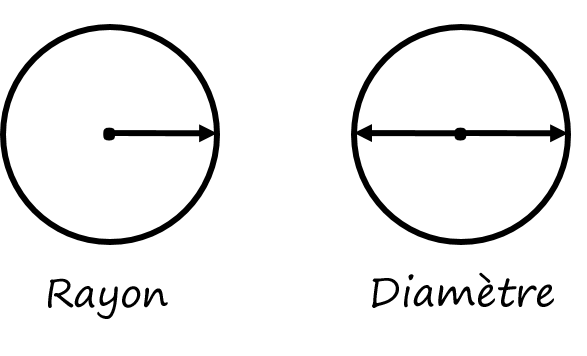
Il est intéressant de noter qu’il existe deux façons différentes de trouver l’aire d’un cercle. L’une comprend l’utilisation du rayon et l’autre l’utilisation du diamètre. Les deux équations fonctionnent aussi bien l’une que l’autre, mais en général, lorsqu’il s’agit des métiers, on utilise la formule du diamètre.

Souvenez-vous qu’à un moment donné, dans un autre chapitre, j’ai expliqué qu’apprendre à comprendre les concepts pouvait aider à éliminer le besoin de mémoriser des formules. Ce fait anecdotique peut vous aider à comprendre l’aire d’un cercle.
La première étape du processus consiste à prendre un cercle et à l’insérer parfaitement dans un carré.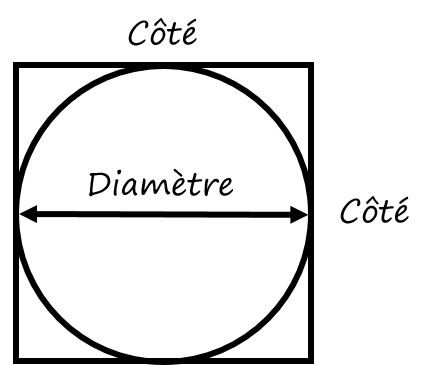
Vous remarquerez que le côté du carré est de la même longueur que le diamètre du cercle.
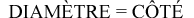
Voici le fait anecdotique!
Il s’avère que l’aire d’un cercle placé parfaitement à l’intérieur d’un carré occupe exactement 78,54 pour cent de l’aire du carré.
C’est grâce à cette information que nous pouvons trouver la formule de l’aire d’un cercle.
Si la formule pour l’aire d’un carré est côté × côté, alors si nous prenons 78,54 pour cent de cette réponse, nous obtiendrons l’aire du cercle.
Comme le diamètre est de la même longueur que le côté, nous pouvons dire que le diamètre × le diamètre nous donne l’aire du carré et qu’en prenant 78,54 % de ce chiffre, nous obtenons l’aire du cercle.
Heureusement pour nous, le diamètre est l’une des caractéristiques d’un cercle que nous utiliserons.
Après cette longue explication, nous en arrivons à ceci :

Dans cette formule, 0,7854 représente les 78,54 pour cent dont nous avons parlé plus tôt.
Cette équation vous rappelle peut-être une autre équation pour l’aire d’un cercle et bien, votre souvenir est correct. La formule ci-dessus est celle que nous utilisons pour les métiers, mais si vous utilisiez la formule ci-dessous, vous auriez également raison.
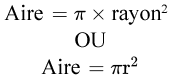
Dans ce cas, π est une constante. Tel qu’indiqué précédemment, cette formule est également correcte, mais en général, lorsque l’on utilise les mathématiques pour les métiers, on s’en tient à la formule utilisant le diamètre.
Exemple
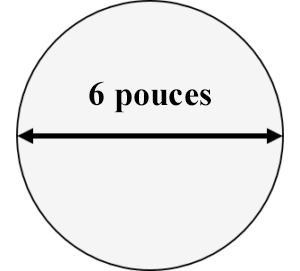
Quelle est l’aire d’un cercle dont le diamètre est de 6 pouces?
Étape 1 : Écrivez la formule.
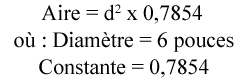
Étape 2 : Saisissez les variables et trouvez l’aire.
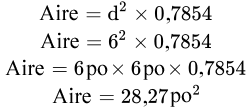
N’oubliez pas qu’en calculant la surface d’un objet bidimensionnel, notre réponse finit par être élevée au carré. Une fois de plus, les pouces au carré représentent deux dimensions. Avant de passer à un autre exemple, essayons de répondre à la même question, mais en utilisant l’autre formule pour calculer l’aire.
Étape 1 : Écrivez la formule.
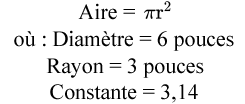
Étape 2 : Saisissez les variables et trouvez l’aire.
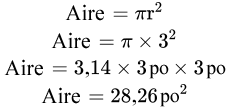
Comme vous pouvez le voir, les deux formules donnent la même réponse. Bien que dans toutes les questions nous utilisions la formule du diamètre, n’hésitez pas à utiliser la formule du rayon. En fin de compte, ce qui importe, c’est que vous compreniez le processus et que vous obteniez la bonne réponse.
Exemple
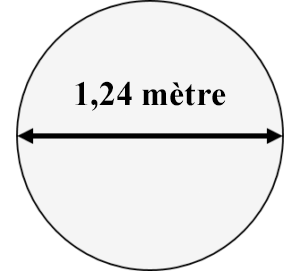 Quelle est la surface d’un cercle dont le diamètre est de 1,24 m?
Quelle est la surface d’un cercle dont le diamètre est de 1,24 m?Étape 1 : Écrivez la formule.
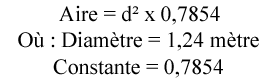
Étape 2 : Saisissez les variables et trouvez l’aire.
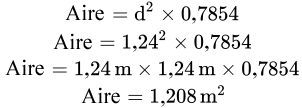
Exercice pratique
Essayez de faire un exercice pratique seul.e. Assurez-vous de consulter les réponses vidéo pour voir comment vous vous êtes débrouillé.
Exercices

Jascarn installe des luminaires encastrés de 6 pouces au plafond de la maison d’un ami. Quelle est l’aire du trou que Jascarn devra découper pour y insérer un luminaire encastré de 6 pouces de diamètre?