Volume d’une sphère

eCampusOntario

Volume

17 Volume d’une sphère

Sélectionnez le lecteur audio suivant pour écouter en lisant cette section.

Un élément de BCcampus a été exclu de la présente version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades2/?p=225

Nous avons à gauche une photo de notre belle planète, la Terre. Bien que l’image elle-même soit bidimensionnelle, nous savons que la Terre est tridimensionnelle. La Terre a un volume. La Terre est également un exemple de sphère.

Jusqu’à présent, nous avons calculé le volume des cubes, des réservoirs rectangulaires et des cylindres. À l’aide de ces informations, comment pensez-vous que nous pourrions calculer le volume d’une sphère? Quelles variables pensez-vous utiliser? Réfléchissez quelques minutes avant de passer à l’explication ci-dessous.

Au cas où vous vous poseriez la question, la Terre a un volume de…

$\Large 1,083,206,916,846 \text{ cubic kilometres}$

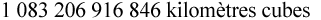
Il y a deux choses à noter ici :

La réponse est encore une fois en unités cubiques.
C’est beaucoup de volume.

Nous devrions commencer par réexaminer la formule d’un cercle. Souvenez-vous qu’un cercle a un rayon, un diamètre et une circonférence. Souvenez-vous aussi que pour trouver la formule d’un cercle, nous aurions pu utiliser l’une des deux formules.

$\Large \begin{array}{ll} \text{Formula one:} & \text{ area} = {\text{d}}^ \times 0.7854 \times \text{h} \\ \text{Formula two:} & \text{ area} = \pi {\text{r}}^ \end{array}$

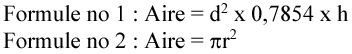
Lorsque nous abordons la formule pour une sphère, nous pouvons utiliser la formule deux comme point de départ. La formule d’une sphère a un aspect semblable, mais avec une petite particularité. Les similitudes comprennent le fait d’avoir à la fois pi et le rayon dans la formule, mais c’est là que les similitudes s’arrêtent.

Voici la formule :

$\Large \text{volume} = \dfrac \pi {\text{r}}^$

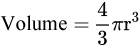
La question devient : « D’où viennent les 4/3? » Eh bien, l’explication est en fait assez longue, et je la laisse pour un autre jour. En bref, cela vient du fait que si l’on prend deux cônes ayant des dimensions similaires à celles de la sphère, le volume de ces deux cônes sera égal à celui de la sphère. Avec un peu d’astuce mathématique le 4/3 découle de ce fait.

Une sphère et deux cônes d’à peu près la même taille.

Le pi dans la formule est la constante que nous utilisons pour trouver la circonférence d’un cercle, et le rayon, comme vous vous en souvenez peut-être, équivaut à la moitié de la longueur du diamètre. Et enfin, le rayon est au cube. Cela est lié au fait qu’en fin de compte, nous calculons un volume, qui a trois dimensions.

Je ne m’attendais pas à ce que vous compreniez la formule, car elle est assez bizarre, mais le fait de comprendre d’où elle vient aide à la conceptualiser. Comme nous en avons parlé précédemment, le but de cet exercice est de s’appuyer moins sur la mémorisation et plus sur la compréhension de la manière dont les choses sont calculées.

Exemple

Calculez le volume d’une sphère dont le rayon est de 7 pouces.

Étape 1 : Comme d’habitude, écrivez la formule.

$\Large \text{volume} = \dfrac \pi {\text{r}}^$

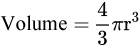
Étape 2 : Insérez les variables et calculez le volume

$\Large \begin{array}{c}\text{volume} = \dfrac \pi {\text{r}}^ \\ \text{volume} = \dfrac \pi ^ \\ \text{volume} = \dfrac \times \pi \times 7 \times 7 \times 7 \\ \text{volume}= 1436{\text{ in}}^ \end{array}$

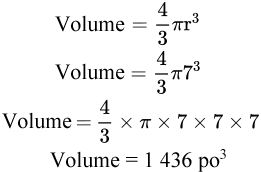
Exemples

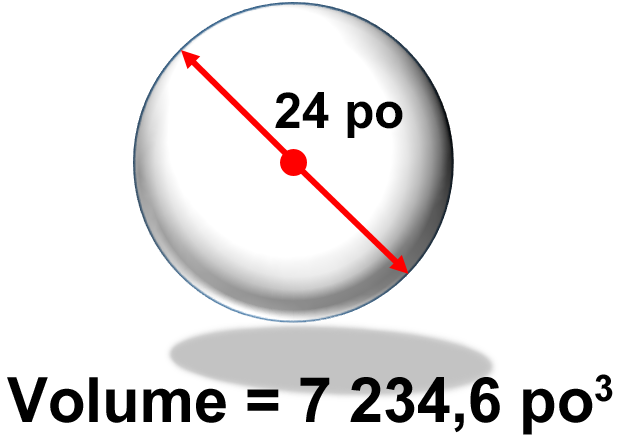
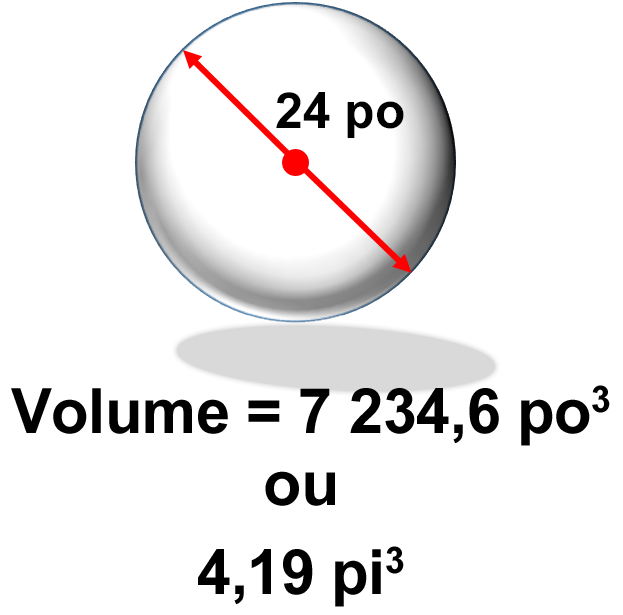
Allons un peu plus loin et ajoutons un élément de plus. Calculez le volume d’une sphère dont le diamètre est de 24. Notez que le diamètre doit passe par le centre exact de la sphère. Pensez à l’endroit où vous vous trouvez en ce moment, et percez un trou tout droit à travers la Terre jusqu’à l’autre côté, en vous assurant de passer par le centre de la Terre. (Avertissement : Je pense qu’il y a le scénario d’un film d’Arnold Schwarzenegger quelque part dans cette question). Bref, revenons à la question.

Étape 1 : Comme d’habitude, écrivez la formule.

$\Large \text{volume} = \dfrac \pi {\text{r}}^$

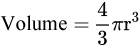
Je suppose qu’à ce stade du livre, vous avez commencé à voir certains schémas et que vous avez remarqué que nous devons utiliser le rayon dans la formule, mais que nous n’avons que le diamètre. Avec un peu d’astuce mathématique, nous allons calculer le rayon à partir du diamètre avant de commencer.

$\Large \begin{array}{c}\text{diameter} = \text{radius} \times 2 \\ \text{radius} = \dfrac{\text{diameter}} \\ \text{radius} = \dfrac \\ \text{radius} = 12 \end{array}$

Nous avons maintenant ce qu’il nous faut pour travailler.

Étape 2 : Insérez les variables et calculez le volume.

$\Large\begin{array}{c} \text{volume} = \dfrac \pi {\text{r}}^ \\ \text{volume} = \dfrac \pi ^ \\ \text{volume} = \dfrac \times \pi \times 12 \times 12 \times 12 \\ \text{volume}= 7234.6 {\text{ in}}^ \end{array}$

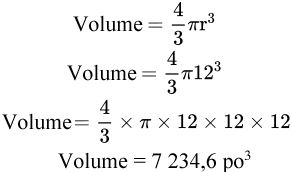
Hé! Faut-il ajouter une question en prime ici? Alors, allons-y. Changer le volume des pouces cubes en pieds cubes.

Étape 1 : Écrivez la formule.

$\Large 1 \text{ cubic foot} = 1728 \text{ cubic inches}$

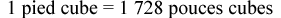
Étape 2 : Faites une multiplication croisée.

$\Large \begin{array}{c}\dfrac{1 {\text{ ft}}^}{{\text{X ft}}^} = \dfrac{1728 {\text{ in}}^}{7234.6 {\text{ in}}^} \\ 1 \times 7234.6 = \text{X} \times 1728 \\ \text{X} = \dfrac{7234.6} \\ \text{X} = 4.19{\text{ ft}}^ \end{array}$

le volume est égal à 7 234,6 pouces cubes ou 4,19 pieds cubes

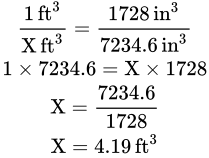
Exercice pratique

Essayez de répondre seul.e à un exercice pratique, et vérifiez la réponse vidéo pour voir si vous avez bien répondu à la question.

Question 1

Josh et Jatinder sont tous les deux partisans de la NBA et en classe ils discutent de ce que le volume d’un ballon de basketball pourrait être. Ils ont calculé que le diamètre d’un ballon de basket est de 9,5 pouces. Calculer le volume d’un ballon de basketball.

Un élément de BCcampus a été exclu de la présente version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades2/?p=225

Licence

Symbole de Licence Creative Commons Attribution 4.0 International

Exercice pratique

Licence

Partagez ce livre