Volume
16 Volume d’un cylindre
Sélectionnez le lecteur audio suivant pour écouter en lisant cette section.

À votre avis, que contient le réservoir sur la photo de gauche?
Peut-être de l’eau? Peut-être des céréales? Peut-être des vieux manuels de mathématiques pour les métiers de la construction?

Pour nous, en ce moment, il est moins important de savoir ce qu’il y a dans le réservoir que de savoir comment calculer la quantité de choses qui peuvent entrer dans le réservoir.
Ce type de réservoir est connu sous le nom de cylindre et se compose de trois éléments. Il comporte un sommet, un fond et une partie centrale. Nous supposerons que le haut et le bas sont tous deux des cercles parfaits de même diamètre et de même surface.

Un réservoir d’eau chaude est un bon exemple de cylindre. Examinez le réservoir d’eau chaude à droite et réfléchissez à ce que vous pourriez avoir besoin de savoir si vous deviez calculer son volume.
Qu’avez-vous trouvé? Et si vous essayiez de trouver une formule? Je vous donne un indice avant que vous ne tentiez votre chance.
Astuce : Le volume a une forme cubique. Par exemple : pieds cubes, mètres cubes, pouces cubes, etc.

Formule pour calculer le volume d’un cylindre
Voici la formule.
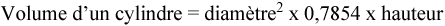

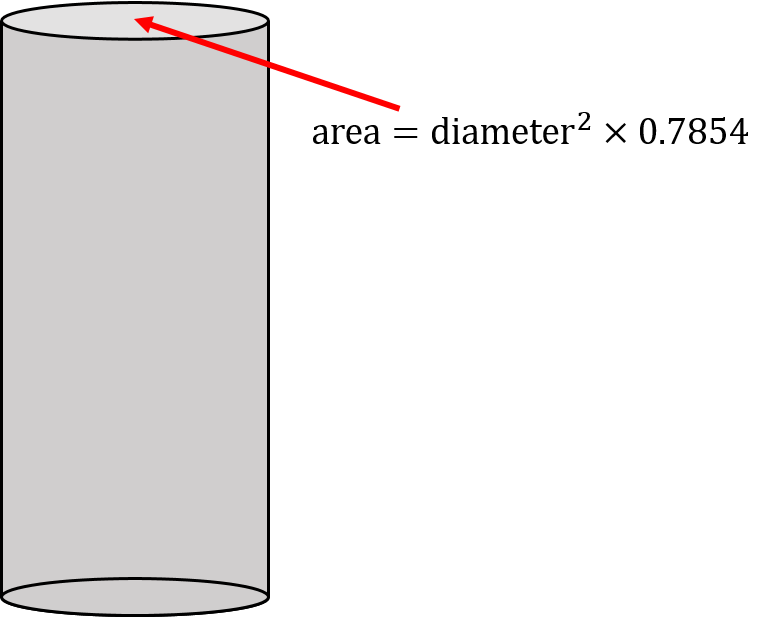
Le sommet d’un cylindre est tout simplement un cercle. Il comporte un diamètre, un rayon et une circonférence. Le fond et le sommet du réservoir ont les mêmes dimensions.
Nous avons donc besoin de cet élément (l’aire du sommet ou du fond) comme point de départ.
La question qui se pose est : « Quelle est la hauteur ou la longueur du réservoir? »
Cela jouera également un rôle important dans le calcul du volume.
Mettez tout cela ensemble et vous obtenez votre formule :
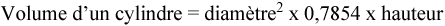
Une dernière question :

Quel genre et quel type d’unités allons-nous traiter dans notre réponse?
Des unités pour le volume d’un cylindre
Cette réponse comporte en réalité deux volets.
Première partie
La réponse à cette question se trouve dans toutes les unités des variables que nous traitons. Si nous avons affaire à des pieds, notre réponse sera la version en pieds. Si nous avons affaire à des pouces, notre réponse sera la version en pouces.

Notez que vous avez deux variables différentes, le diamètre et la hauteur. Assurez-vous que les deux variables sont dans les mêmes unités lors de l’élaboration de votre réponse. Si le diamètre est en pouces et la hauteur est en pieds, vous devez convertir l’un ou l’autre de sorte qu’ils soient tous les deux la même unité.
Deuxième partie
Tel qu’énoncé plus tôt, notre réponse sera en unités cubiques. Bien que nous n’ayons que deux variables (diamètre et hauteur), le diamètre est au carré et nous pourrions donc écrire la formule comme suit :
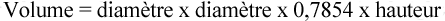
Au bout du compte, nous aurons trois variables, dont deux sont identiques. C’est ainsi que nous obtenons notre réponse en unités cubiques (3).
Exemples
Un réservoir cylindrique a un diamètre de 7 pouces et une hauteur de 51 pouces. Quel est le volume du réservoir?
Étape 1 : écrivez la formule et trouvez les variables.


Maintenant, avant de continuer, vérifiez et assurez-vous que les variables sont dans des unités semblables. Si elles sont différentes, il faudra les modifier pour qu’elles soient toutes les mêmes.
Par chance, dans cette question, elles sont toutes les deux en pouces, donc nous pouvons y aller.
Étape 2 : Insérez les variables dans la formule et répondez à la question.
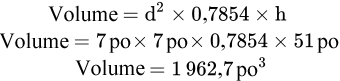
Exemple
Calculez le volume d’un réservoir cylindrique qui a un diamètre de 555 millimètres et une hauteur de 7,9 mètres.
Étape 1 : Écrivez la formule et trouvez les variables.


Les deux variables sont dans des unités différentes. Il faut modifier l’une ou l’autre pour mettre les deux dans les mêmes unités. Dans ce cas-ci, nous travaillerons avec des mètres et notre réponse sera en mètres cubes.

La hauteur de 7,9 mètres nous convient, mais pas le diamètre de 555 millimètres. Nous devons les convertir en mètres pour que tout soit cohérent.
Nous devons revenir quelques chapitres en arrière et puiser dans mémoire.
Rappelez-vous que 1 mètre = 1 000 millimètres.
Pour calculer le nombre de mètres dans 555 millimètres, nous procédons comme suit :

Maintenant que les deux variables sont dans des unités semblables, nous pouvons aller de l’avant et calculer le volume.
Étape 2 : Insérez les variables dans la formule et répondez à la question.
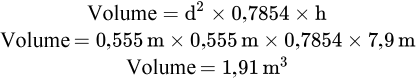
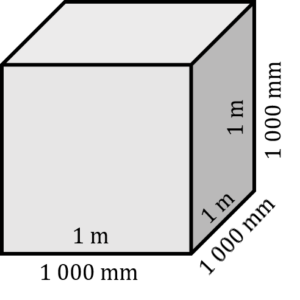
Nous avons donc notre réponse en mètres cubes, mais que se passerait-il si nous voulions modifier cette réponse en millimètres cubes? Reprenons notre dessin d’un cube pour trouver la relation entre les mètres cubes et les millimètres cubes.
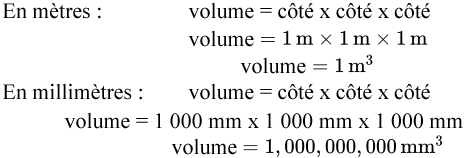
Au final, un mètre cube équivaut donc à beaucoup de millimètres cubes. Plus précisément, un mètre cube équivaut à un milliard de millimètres cubes.
Alors combien de millimètres cubes y a-t-il dans notre réservoir cylindrique dans l’exemple ci-dessus?
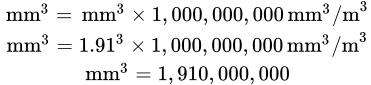
Exercices pratiques
Essayez quelques exercices pratiques pour vous-même. Assurez-vous de consulter les réponses vidéo pour voir comment vous vous êtes débrouillé.
Question 1

Gerrard va installer un nouveau chauffe-eau. Le réservoir a un diamètre de 1 pied 3 pouces et une hauteur de 5 pieds 2 pouces. Quel est le volume du réservoir en pieds cubes?
Question 2

Un pot de peinture d’un gallon mesure environ 6½ pouces de diamètre et 7½ pouces de hauteur. Un gallon suffit pour peindre jusqu’à 400 pieds carrés, ce qui correspond à peu près à la surface d’une petite salle de bains.
Calculez le volume du pot de peinture en pouces cubes et en pieds cubes.

