"

1.4. Rapports, taux et pourcentages

Rapports et taux

Rapport : relation entre deux nombres, exprimée sous forme de quotient avec la même unité au dénominateur et au numérateur. Il existe trois façons d’écrire un rapport.

Exemple : Écrire le rapport entre 5 cents et 9 cents.

 

  • Simplifier un rapport :

 

Taux : rapport entre deux quantités d’unités différentes.

Exemple : enseignants à étudiants; argent à temps; distance à temps, etc.

Exemple : 80 kilomètres pour 320 minutes :      \frac{\bcancelkm}{\bcancelmin}=\frac{1km}{4min}

 

Taux unitaire : taux dans lequel le nombre au dénominateur est 1.

Exemple :  15 dollars par heure           \frac{\$15}{1h} = 15 $ par heure
  • Voici quelques taux unitaires :

Proportion : équation dont les deux côtés présentent un rapport (ou un taux) (\frac{a}{b}=\frac{c}{d}).

Exemple : Transformons la phrase suivante en proportion.

3 imprimantes correspondent à 18 ordinateurs, tandis que 2 imprimantes correspondent à 12 ordinateurs.

\frac{3\;imprimantes}{18\;ordinateurs}=\frac{2\;imprimantes}{12\;ordinateurs}

 

Résolution d’une proportion :

  • Multiplication croisée : multiplier le long de deux diagonales.  \frac{a}{b}=\frac{c}{d}
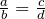
  • Trouver la valeur de l’inconnue.

 

4 litres de lait coûtent 4,38 $, combien coûtent 2 litres ?

  • Faits et inconnue :
4 L de lait 2 L de lait
4,38 $ x $ = ?
  • Proportion :
 \frac{4\;L}{\$4.38}=\frac{2\;L}{\$x}
  • Multiplication croisée :
 (4)(x)=(2)(4,38)
  • Trouver la valeur de x :
 \frac{\bcancelx}{\bcancel}=\frac{2(4.38)} Diviser les deux côtés par 4.
x=\frac{(2)(4.38)}=2.19
2 litres de lait coûtent 2,19 dollars.
  • Vérifier :
 \frac{4\;L}{\$4.38}=\frac{2\;L}{\$2.19} Remplacer x par 2,19.
(4) (2,19) = (2) (4,38)
8,76 = 8,76 Bonne réponse!

 

Tom mesure 1,75 mètre et son ombre mesure 1,09 mètre. L’ombre d’un bâtiment mesure 10 mètres de long au même moment. Quelle est la hauteur du bâtiment?

  • Faits et inconnue :
    Taille de Tom = 1,75 m   Hauteur du bâtiment (x) = ?
    Ombre de Tom = 1,09 m   Ombre du bâtiment = 10 m
  • Proportion :
 \frac{1.75m}{1.09m}=\frac{xm}{10m}
  • Multiplication croisée :
 (1.75)(10)=(1.09)(x)
  • Trouver la valeur de x :
 x=\frac{(1.75)(10)}{1.09}=\frac{(\bcancel{1.09})x}{\bcancel{1.09}} Diviser les deux côtés par 1,09.
x=\frac{(1.75)(10)}{1.09}\approx16.055
La hauteur du bâtiment est de 16,055 m.
  • Vérifier :
 \frac{1.75m}{1.09m}=\frac{16.055m}{10m} Remplacer x par 16,055.
(1.75) (10) = (16.055) (1.09)
17,5 = 17,5 Bonne réponse!

 

Si 15 mL de médicament doivent être mélangés à 180 mL d’eau, combien de millilitres de médicament doivent être mélangés à 230 mL d’eau?

  • Proportion :
 \frac{15\;mL}{180\;mL}=\frac{x\;mL}{230\;mL} \frac{15\;mL\;médicament}{180\;mL\;eau}=\frac{x\;mL\;médicament}{230\;mL\;eau}
  • Multiplication croisée :
 (15)(230)=(180)(x)
  • Trouver la valeur de x :
 x=\frac{(15\;mL)(230\;mL)}{180\;mL}\approx19,17\;mL
19,17 mL de médicament doivent être mélangés à 230 mL d’eau.

 

Pourcentage

Pourcentage (%) : une partie pour cent.

Conversion entre pourcentages, décimales et fractions :

Conversion Étapes Exemples
Pourcentage ⇒ Décimale Déplacer la virgule de deux positions vers la gauche, puis supprimer le symbole %. 31 %  =  31, % = 0,31
Décimale ⇒ Pourcentage Déplacer la virgule de deux positions vers la droite, puis ajouter le symbole %. 0,317 = 0, 317 = 31,7 %
Pourcentage ⇒ Fraction Enlever le %, diviser par 100, puis simplifier.  15 % = \frac=\frac
Fraction ⇒ Pourcentage Diviser, déplacer la virgule de deux positions vers la droite, puis ajouter le symbole %. \frac = 1 ÷ 4 = 0,25 = 25 %
Décimale ⇒ Fraction Convertir la décimale en pourcentage, puis convertir le pourcentage en fraction. 0,35 = 35 % = \frac=\frac

% = pour cent

 

Il existe deux méthodes pour résoudre les problèmes de pourcentage :

  • Méthode des proportions en pourcentage
  • Traduction (traduire les mots en symboles mathématiques).

 

Méthode des proportions en pourcentage :

\frac{Partie}{Tout}=\frac{Pour cent} ou \frac{nombre\;« est »}{nombre\;« de »}=\frac{\%}

 

Étapes Exemples
8 pour cent de quel nombre est 4?
  • Déterminer la partie, le tout et le pourcentage.
 ⇑

Pourcentage

 ⇑

Tout (x)

 ⇑

Partie
  • Établir l’équation de la proportion.
 \frac{x}=\frac \frac{Partie}{Tout}=\frac{\%}
  • Trouver la valeur de l’inconnue (x).
 x=\frac{(4)(100)}=50 x = 50

Méthode de traduction : traduire les mots en symboles mathématiques.

  • Quel ____ x = : le mot « quel » correspond à la quantité inconnue x.
  • est ____  = : le verbe « est » correspond au signe d’égalité.
  • de ____ × : le mot « de » correspond au signe de multiplication.
  • %  : toujours transformer le pourcentage en nombre décimal.

 

1) Quel est 15 % de 80?

                       x  =  0,15 • 80                         x = (0,15)(80) = 12  

 2)   Quel pourcentage de 90 est 45?

                      x % • 90 = 45                          x % = \frac = 0,5 = 50 %                       

 3)  12 est 8 % de quel nombre?

                      12 = 0,08 • x                          x = \frac{0.08} = 150                               

 

Pourcentage d’augmentation ou de diminution :

Application Formule
Pourcentage d’augmentation Pourcentage d’augmentation = \frac{Nouvelle\;valeur-Valeur\;originale}{Valeur\;originale} x=\frac{N-O}{O}
Pourcentage de réduction Pourcentage de diminution = \frac{Valeur\;originale-Nouvelle\;valeur}{Valeur\;originale} x=\frac{O-N}{O}

 

La production d’un bien est passée de 1 500 unités le mois dernier à 1 650 ce mois-ci.  Trouvez le pourcentage d’augmentation.

Nouvelle valeur (N) 1 650 Ce mois-ci.
Valeur originale (O) : 1 500 Le mois dernier.
Pourcentage d’augmentation : x=\frac{N-O}{O}=\frac{1650-1500}=0,1=10\%} Une augmentation de 10 %.

 

La production a été réduite de \bf{\$}33 à \bf{\$}29.  Quel est le pourcentage de réduction?

Pourcentage de réduction : x=\frac{O-N}{O}=\frac{33-29}\approx0,12=12\% Une réduction de 12 %.

 

Exercices pratiques

1. Exprimez les données suivantes sous forme de rapport ou de taux simplifié.

2. Un train a parcouru 459 km en 6 heures. Quel est le taux unitaire?

3. Exprimez la phrase suivante à l’aide d’une proportion : 24 heures correspondent à 1 940 kilomètres et 12 heures à 985 kilomètres.   

4. 4 litres de jus de fruit coûtent 7,38 $. Combien coûtent 2 litres?

5. Sarah gagne 4 500 $ en 30 jours. Combien gagne-t-elle en 120 jours?

6. Un produit a vu sa production passer de 2 800 unités l’année dernière à 3 920 unités cette année. Trouvez le pourcentage d’augmentation.

7. Le tableau ci-dessous présente des données sur le chômage des étudiants en santé publique de l’Université métropolitaine de Toronto durant l’été, mais certaines données sont manquantes :

Année 2015 2016 2017
Étudiants au chômage 350 ? 396
Nombre total d’étudiants 1 250 1 100 ?

 

 

Licence

Symbole de License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International

Mathématiques pour les professions de la santé publique et au travail Droit d'auteur © 2024 par eCampusOntario est sous licence License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, sauf indication contraire.

Partagez ce livre