6.4 Skewness
Learning Objectives
- Identify the shape of a set of data.
Symmetrical Distribution
Consider the following data set:
| 4 | 5 | 6 | 6 | 6 | 7 | 7 | 7 |
| 7 | 7 | 7 | 8 | 8 | 8 | 9 | 10 |
This data set can be represented by the following histogram. Each interval has width one, and each value is located in the middle of an interval.
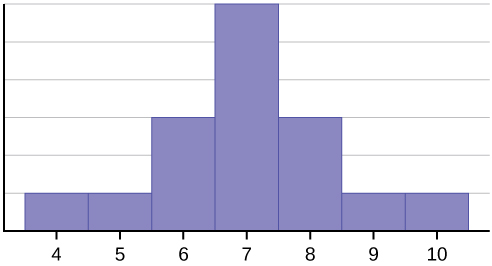
Image Description
A histogram with data values ranging from 4 to 10 along the x-axis. The y-axis represents the frequency of occurrences within each bin, though specific frequency values are not labelled. The histogram has the following distribution:
- Values at 4 and 10 have lower frequencies.
- Frequencies increase for values at 6 and 8.
- The highest frequency occurs at the value 7, forming a peak in the center.
- The distribution appears roughly symmetrical, centred around the value 7.
The histogram above displays a symmetrical distribution of data. A distribution is symmetrical if a vertical line can be drawn at some point in the histogram so that the shapes to the left and the right of the vertical line are mirror images. For the above data set, the mean, the median, and the mode are each seven. In a perfectly symmetrical distribution, the mean and the median are the same. This example has one mode, and the mode is the same as the mean and median. In a symmetrical distribution that has multiple modes, the modes would be different from the mean and median.
Left Skewed Distribution
Consider the following data set:
| 4 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 |
This data set can be represented by the following histogram. Each interval has width one, and each value is located in the middle of an interval.
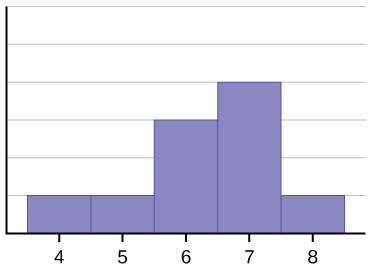
Image Description
A histogram displaying data values from 4 to 8 on the x-axis. The y-axis indicates frequency, though specific frequency values are not shown. The histogram has the following characteristics:
- Lower frequencies are observed at values 4, 5, and 8.
- Frequencies increase at values 6 and 7, with the highest frequency at 7.
- The distribution is skewed slightly towards the higher end, with a peak at 7.
The histogram above is not symmetrical. The right-hand side seems "chopped off" compared to the left side. A distribution of this type is called skewed to the left because it is pulled out to the left. The mean of this data is 6.3, the median is 6.5, and the mode is 7. Notice that the mean is less than the median, and they are both less than the mode. The mean and the median both reflect the skewing, but the mean reflects it more so.
Right Skewed Distribution
Consider the following data set:
| 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 10 |
This data set can be represented by the following histogram. Each interval has width one, and each value is located in the middle of an interval.
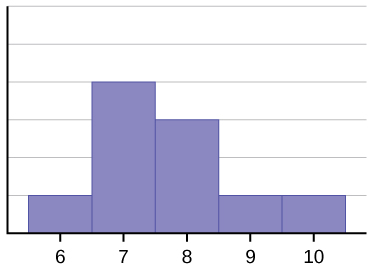
Image Description
A histogram with data values ranging from 6 to 10 on the x-axis. The y-axis represents frequency, although specific values are not labelled. The histogram's distribution shows:
- Lower frequencies at values 9 and 10.
- Higher frequencies at values 7 and 8, with the highest peak at 7.
- The distribution is slightly skewed to the right, with most data clustered around 7 and 8.
The histogram above is also not symmetrical. In this case, the data is skewed to the right. The mean for this data is 7.7, the median is 7.5, and the mode is 7. Of the three statistics, the mean is the largest, while the mode is the smallest. Again, the mean reflects the skewing the most.

- If the distribution of the data is symmetrical, [latex]\mbox{mean}=\mbox{median}=\mbox{mode}[/latex] (assuming there is only one mode). If there are multiple modes in a symmetric distribution, the modes would be different from the mean and the median, but the mean and median would still be equal.
- If the distribution of the data is skewed to the left, [latex]\mbox{mean} \lt \mbox{median} \lt \mbox{mode}[/latex].
- If the distribution of the data is skewed to the right, [latex]\mbox{mean} \gt \mbox{median} \gt \mbox{mode}[/latex].
Video: Elementary Business Statistics | Skewness and the Mean, Median, and Mode by Janux [3:58] is licensed under the Standard YouTube License.Transcript and closed captions available on YouTube.
Example 6.4.1
Statistics are used to compare and sometimes identify authors. The following list shows a simple random sample that compares the letter counts for three authors.
| Terry | |||||||||
| 7 | 9 | 3 | 3 | 3 | 4 | 1 | 3 | 2 | 2 |
| Davis | |||||||||
| 3 | 3 | 3 | 4 | 1 | 4 | 3 | 2 | 3 | 1 |
| Maris | |||||||||
| 2 | 3 | 4 | 4 | 4 | 6 | 6 | 6 | 8 | 3 |
- Make a dot plot for the three authors and compare the shapes.
- Calculate the mean for each.
- Calculate the median for each.
- Describe any pattern you notice between the shape and the measures of center.
Solution:
-

Terry’s distribution has a right (positive) skew. 
Davis’ distribution has a left (negative) skew 
Maris’ distribution is symmetrically shaped. - Terry’s mean is 3.7, Davis’ mean is 2.7, Maris’ mean is 4.6.
- Terry’s median is three, Davis’ median is three. Maris’ median is four.
- It appears that the median is always closest to the high point (the mode), while the mean tends to be farther out on the tail. In a symmetrical distribution, the mean and the median are both centrally located close to the high point of the distribution.
Attribution
"2.4 Skewness and the Mean, Median, and Mode" in Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

