6.3 Descriptive Measures
Learning Objectives
- Calculate the mean, median, mode, range, variance, standard deviation, Standard Error of the Means, and Coefficient of Variation for any population or sample.
- Identify symmetric distribution and skewed sets.
Formula & Symbol Hub
Symbols Used
- [latex]\mu[/latex] = Population mean
- [latex]\sigma^2[/latex] = Population variance
- [latex]\sigma[/latex] = Population standard deviation
- [latex]\bar{x}[/latex] = Sample Mean
- [latex]s^2[/latex] = Sample variance
- [latex]s[/latex] = Sample standard deviation
- [latex]s_{\bar{x}}[/latex] = Standard error of the means
Formulas Used
-
Formula 6.1 - Population Mean
[latex]\begin{align*}\mu&=\frac{\sum x_i}{N}\end{align*}[/latex]
-
Formula 6.2 - Sample mean
[latex]\begin{align*}\bar{x}&=\frac{\sum x_i}{n}\end{align*}[/latex]
-
Formula 6.3 - Population Variance
[latex]\begin{align*}\sigma^2=\frac{\sum\left(x_i-\mu\right)^2}{N}\end{align*}[/latex]
-
Formula 6.4 - Sample Variance
[latex]\begin{align*}s^2=\frac{\sum\left(x_i-\bar{x}\right)^2}{n-1}=\frac{\Sigma x_i^2-\frac{\left(\sum x_i\right)^2}{n}}{n-1}\end{align*}[/latex]
-
Formula 6.5 - Population Standard Deviation
[latex]\sigma=\sqrt{\sigma^2}[/latex]
-
Formula 6.6 - Sample Standard Deviation
[latex]s=\sqrt{s^2}[/latex]
-
Formula 6.7 - Standard Error of the Means
[latex]\begin{align*}s_{\bar{x}}=\sqrt{\frac{s^2}{n}}=\frac{s}{\sqrt{n}}\end{align*}[/latex]
-
Formula 6.8 - Coefficient of Variation (Population)
[latex]\begin{align*}CV=\frac{\sigma}{\mu}\times 100\end{align*}[/latex]
-
Formula 6.9 - Coefficient of Variation (Sample)
[latex]\begin{align*}CV=\frac{s}{\bar{x}}\times 100\end{align*}[/latex]
Descriptive measures of populations are called parameters and are typically written using Greek letters. The population mean is [latex]\mu[/latex] (mu). The population variance is [latex]\sigma^2[/latex] (sigma squared), and population standard deviation is [latex]\sigma[/latex] (sigma).
Descriptive measures of samples are called statistics and are typically written using Roman letters. The sample mean is [latex]\bar{x}[/latex](x-bar). The sample variance is [latex]s^2[/latex] and the sample standard deviation is [latex]s[/latex]. Sample statistics are used to estimate unknown population parameters.
In this section, we will examine descriptive statistics in terms of measures of center and measures of dispersion. These descriptive statistics help us to identify the center and spread of the data.
Measures of Center
Mean
The arithmetic mean of a variable, often called the average, is computed by adding up all the values and dividing by the total number of values.
The population mean is represented by the Greek letter [latex]\mu[/latex] (mu). The sample mean is represented by [latex]\bar{x}[/latex](x-bar). The sample mean is usually the best, unbiased estimate of the population mean. However, the mean is influenced by extreme values (outliers) and may not be the best measure of center with strongly skewed data. The following equations compute the population mean and sample mean.
[latex]\boxed{6.1}[/latex] Population Mean
[latex]\begin{align*}\color{blue}{\mu}&=\frac{\sum \color{red}{x_i}}{\color{green}{N}}\end{align*}[/latex]
[latex]\boxed{6.2}[/latex] Sample Mean
[latex]\begin{align*}\color{blue}{\bar{x}}&=\frac{\sum \color{red}{x_i}}{\color{green}{n}}\end{align*}[/latex]
[latex]{\color{red}{x_i}}\text{ is an element in the data set.}[/latex]
[latex]{\color{blue}{\mu}}\text{ and }{\color{blue}{\bar{x}}}\text{ are the population and sample means:}[/latex] the averages of all values in their respective data sets.
[latex]{\color{green}{N}}\text{ and }{\color{green}{n}}\text{ are the number of elements in the data set: }{\color{green}{N}}[/latex] is used for calculations of the population mean while [latex]{\color{green}{n}}[/latex] is used for calculations of the sample mean.
Try It
Find the mean for the following sample data set: [latex]6.4, 5.2, 7.9, 3.4[/latex]
Solution
[latex]\begin{align*}\bar{x}=\frac{6.4+5.2+7.9+3.4}{4}=5.725\end{align*}[/latex]
Median
The median of a variable is the middle value of the data set when the data are sorted in order from least to greatest. It splits the data into two equal halves, with [latex]50\%[/latex] of the data below the median and [latex]50\%[/latex] above the median. The median is resistant to the influence of outliers and may be a better measure of the center with strongly skewed data.
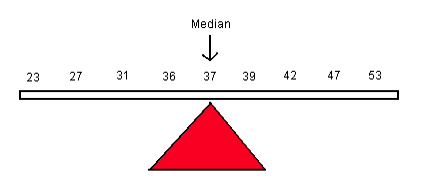
Image Description
The image is a visual representation of a set of numbers balanced on a red triangle, indicating the median value. The numbers, in ascending order from left to right, are [latex]23[/latex], [latex]27[/latex], [latex]31[/latex], [latex]36[/latex], [latex]37[/latex], [latex]39[/latex], [latex]42[/latex], [latex]47[/latex], and [latex]53[/latex]. Above the number [latex]37[/latex], there is an arrow pointing down with the label "Median."
The calculation of the median depends on the number of observations in the data set.
To calculate the median with an odd number of values ([latex]n[/latex] is odd), first sort the data from smallest to largest.
Example 6.2.1
[latex]23, 27, 29, 31, 35, 39, 40, 42, 44, 47, 51[/latex]
The median is [latex]39[/latex]. It is the middle value that separates the lower [latex]50\%[/latex] of the data from the upper [latex]50\%[/latex] of the data.
To calculate the median with an even number of values (n is even), first sort the data from smallest to largest and take the average of the two middle values.
Example 6.2.2
[latex]23, 27, 29, 31, 35, 39, 40, 42, 44, 47[/latex]
[latex]\begin{align*}M=\frac{35+39}{2}=37\end{align*}[/latex]
Mode
The mode is the most frequently occurring value and is commonly used with qualitative data as the values are categorical. Categorical data cannot be added, subtracted, multiplied or divided, so the mean and median cannot be computed. The mode is less commonly used with quantitative data as a measure of center. Sometimes, each value occurs only once, and the mode will not be meaningful.
 Paths to Success
Paths to Success
Understanding the relationship between the mean and median is important. It gives us insight into the distribution of the variable. For example, if the distribution is skewed right (positively skewed), the mean will increase to account for the few larger observations that pull the distribution to the right. The median will be less affected by these extremely large values, so in this situation, the mean will be larger than the median. In a symmetric distribution, the mean, median, and mode will all be similar in value. If the distribution is skewed left (negatively skewed), the mean will decrease to account for the few smaller observations that pull the distribution to the left. Again, the median will be less affected by these extremely small observations, and in this situation, the mean will be less than the median.
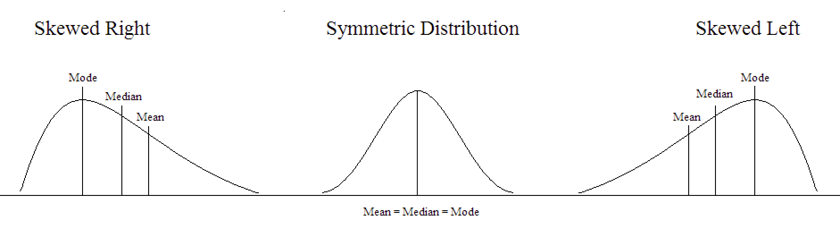
Image Description
The image contains three graphs illustrating different types of data distributions: skewed right, symmetric distribution, and skewed left.
Skewed Right: The graph on the left is labelled "Skewed Right." It shows a distribution where the bulk of the data is concentrated on the left side, with a long tail stretching to the right. Three vertical lines are marked on the graph, indicating the mode (highest point), median, and mean (from left to right). The right tail skews the mean to the right.
Symmetric Distribution: The middle graph is labelled "Symmetric Distribution." It depicts a bell-shaped distribution where the data is evenly distributed around the center. A single vertical line is present at the center of the graph, indicating that the mean, median, and mode are all equal. Below the graph is the notation, "Mean = Median = Mode".
Skewed Left: The graph on the right is labelled "Skewed Left." This graph shows a distribution where the majority of the data is concentrated on the right side, with a long tail extending to the left. Three vertical lines are marked, showing the mean, median, and mode (from left to right). The left tail skews the mean to the left.
Measures of Dispersion
Measures of center look at the average or middle values of a data set. Measures of dispersion look at the spread or variation of the data. Variation refers to the amount of values that vary among themselves. Values in a data set that are relatively close to each other have lower measures of variation. Values that are spread farther apart have higher measures of variation.
Examine the two histograms below. Both groups have the same mean weight, but the values of Group A are more spread out compared to the values in Group B. Both groups have an average weight of [latex]267[/latex] lb. but the weights of Group A are more variable.

Image Description
This image contains two histograms placed side by side.
On the left side, there is a histogram titled "Histogram of Group [latex]A[/latex]."
- The x-axis is labeled "Weight [latex]A[/latex]" and ranges from [latex]20[/latex] to [latex]520[/latex].
- The y-axis is labelled "Frequency" and ranges from [latex]0[/latex] to [latex]35[/latex].
- The histogram shows the distribution of weights in Group [latex]A[/latex], with the tallest bar reaching a frequency of just above [latex]30[/latex] in the weight range of [latex]220-320[/latex]. The frequencies vary between [latex]5[/latex] and [latex]30[/latex] across different weight intervals.
On the right side, there is a histogram titled "Histogram of Group [latex]B[/latex]."
- The x-axis is labeled "Weight [latex]B[/latex]" and ranges from [latex]200[/latex] to [latex]350[/latex].
- The y-axis is labelled "Frequency" and ranges from [latex]0[/latex] to [latex]30[/latex].
- The histogram shows the distribution of weights in Group [latex]B[/latex], with the tallest bar reaching a frequency of just above [latex]25[/latex] in the weight range of [latex]250-275[/latex]. The frequencies vary between [latex]5[/latex] and [latex]30[/latex] across different weight intervals.
Range
The range of a variable is the largest value minus the smallest value. It is the simplest measure and uses only these two values in a quantitative data set.
Try It
Find the range for the given data set.
[latex]12, 29, 32, 34, 38, 49, 57[/latex]
Solution
Range = [latex]57[/latex] – [latex]12 = 45[/latex]
Variance
The variance uses the difference between each value and its arithmetic mean. The differences are squared to deal with positive and negative differences. The sample variance ([latex]s^2[/latex]) is an unbiased estimator of the population variance ([latex]\sigma^2[/latex]), with [latex]n-1[/latex] degrees of freedom.
Degrees of freedom: In general, the degrees of freedom for an estimate is equal to the number of values minus the number of parameters estimated en route to the estimate in question.
The sample variance is unbiased due to the difference in the denominator. If we used [latex]n[/latex] in the denominator instead of [latex]n–1[/latex], we would consistently underestimate the true population variance. To correct this bias, the denominator is modified to [latex]n –1[/latex].
[latex]\boxed{6.3}[/latex] Population Variance
[latex]\begin{align*}{\color{blue}{\sigma^2}}=\frac{\sum\left({\color{red}{x_i}}-{\color{purple}{\mu}}\right)^2}{{\color{green}{N}}}\end{align*}[/latex]
[latex]\boxed{6.4}[/latex] Sample Variance
[latex]\begin{align*}{\color{blue}{s^2}}=\frac{\sum\left({\color{red}{x_i}}-{\color{purple}{\bar{x}}}\right)^2}{{\color{green}{n}}-1}=\frac{\Sigma {\color{red}{x_i}}^2-\frac{\left(\sum {\color{red}{x_i}}\right)^2}{{\color{green}{n}}}}{{\color{green}{n}}-1}\end{align*}[/latex]
[latex]{\color{red}{x_i}}\text{ is an element in the data set.}[/latex]
[latex]{\color{blue}{\sigma^2}}\text{ and }{\color{blue}{s^2}}\text{ are the population and sample variances:}[/latex] the spreads of values in their data sets.
[latex]{\color{green}{N}}\text{ and }{\color{green}{n}}\text{ are the number of elements in a data set: }[/latex] again, [latex]{\color{green}{N}}[/latex] is used for the population data set and [latex]{\color{green}{n}}[/latex] for the sample data set.
[latex]{\color{purple}{\mu}}\text{ and }{\color{purple}{\bar{x}}}\text{ are the population and sample means: }[/latex] these values can be calculated with formulas [latex]6.1[/latex] and [latex]6.2[/latex] respectively
Try It
Compute the variance of the sample data: [latex]3,5,7[/latex]. The sample mean is [latex]5[/latex].
Solution
[latex]\begin{align*}s^2=\frac{\left(3-5\right)^2+\left(5-5\right)^2+\left(7-5\right)^2}{3-1}=4\end{align*}[/latex]
Standard Deviation
The standard deviation is the square root of the variance (both population and sample). While the sample variance is the positive, unbiased estimator for the population variance, the units for the variance are squared. The standard deviation is a common method for numerically describing the distribution of a variable.
[latex]\boxed{6.5}[/latex] Population Standard Deviation
[latex]{\color{red}{\sigma}}=\sqrt{\color{blue}{{\sigma^2}}}[/latex]
[latex]\boxed{6.6}[/latex] Sample Standard Deviation
[latex]{\color{red}{s}}=\sqrt{{\color{blue}{s^2}}}[/latex]
[latex]{\color{red}{\sigma}}\text{ (sigma) and }{\color{red}{s}}\text{ are the population and sample standard deviations. }[/latex]
[latex]{\color{blue}{\sigma^2}}\text{ and }{\color{blue}{s^2}}\text{ are the population and sample variances: }[/latex] these values can be calculated with formulas [latex]6.3[/latex] and [latex]6.4[/latex] respectively.
Try It
Compute the standard deviation of the sample data: [latex]3, 5, 7[/latex] with a sample mean of [latex]5[/latex].
Solution
[latex]\begin{align*}s=\sqrt{\frac{\left(3-5\right)^2+\left(5-5\right)^2+\left(7-5\right)^2}{3-1}}=\sqrt{4}=2\end{align*}[/latex]
Standard Error of the Means
Commonly, we use the sample mean [latex]\bar{x}[/latex] to estimate the population mean [latex]\mu[/latex]. For example, if we want to estimate the heights of eighty-year-old cherry trees, we can proceed as follows:
- Randomly select [latex]100[/latex] trees
- Compute the sample mean of the [latex]100[/latex] heights
- Use that as our estimate
We want to use this sample mean to estimate the true but unknown population mean. But our sample of [latex]100[/latex] trees is just one of many possible samples (of the same size) that could have been randomly selected. Imagine if we take a series of different random samples from the same population and all the same size:
- Sample [latex]1[/latex]—we compute sample mean [latex]\bar{x}[/latex]
- Sample [latex]2[/latex]—we compute sample mean [latex]\bar{x}[/latex]
- Sample [latex]3[/latex]—we compute sample mean [latex]\bar{x}[/latex]
- Etc.
Each time we sample, we may get a different result as we are using a different subset of data to compute the sample mean. This shows us that the sample mean is a random variable!
The sample mean ([latex]\bar{x}[/latex]) is a random variable with its own probability distribution called the sampling distribution of the sample mean. The distribution of the sample mean will have a mean equal to [latex]\mu[/latex] and a standard deviation equal to [latex]\frac{s}{\sqrt{n}}[/latex].
The standard error [latex]\frac{s}{\sqrt{n}}[/latex] is the standard deviation of all possible sample means.
In reality, we would only take one sample, but we need to understand and quantify the sample-to-sample variability that occurs in the sampling process.
The standard error is the standard deviation of the sample means and can be expressed in different ways.
[latex]\boxed{6.7}[/latex] Standard Error of the Means
[latex]\begin{align*}{\color{red}{s_{\bar{x}}}}=\sqrt{\frac{{\color{green}{s^2}}}{{\color{blue}{n}}}}=\frac{{\color{purple}{s}}}{\sqrt{{\color{blue}{n}}}}\end{align*}[/latex]
[latex]{\color{red}{s_\bar{x}}}\text{ is the standard error.}[/latex]
[latex]{\color{blue}{n}}\text{ is the number of values in the sample data set.}[/latex]
[latex]{\color{green}{s^2}}\text{ is the sample variance calculated by formula }6.4[/latex]
[latex]{\color{purple}{s}}\text{ is the sample standard deviation calculated by formula }6.6[/latex]
Example 6.2.3
Describe the distribution of the sample mean.
A population of fish has weights that are normally distributed with [latex]\mu=8[/latex] lb. and [latex]s=2.6[/latex] lb. If you take a sample of size [latex]n=6[/latex], the sample mean will have a normal distribution with a mean of [latex]8[/latex] and a standard deviation (standard error) of [latex]\frac{2.6}{\sqrt{6}}[/latex]= [latex]1.061[/latex] lb.
If you increase the sample size to [latex]10[/latex], the sample mean will be normally distributed with a mean of [latex]8[/latex] lb. and a standard deviation (standard error) of [latex]\frac{2.6}{\sqrt{10}}[/latex] = [latex]0.822[/latex] lb.
Notice how the standard error decreases as the sample size increases.
The Central Limit Theorem (CLT) states that the sampling distribution of the sample means will approach a normal distribution as the sample size increases. If we do not have a normal distribution, or know nothing about our distribution of our random variable, the CLT tells us that the distribution of the [latex]\bar{x}[/latex]’s will become normal as [latex]n[/latex] increases. How large does [latex]n[/latex] have to be? A general rule of thumb tells us that [latex]n\geq 30[/latex].
The Central Limit Theorem tells us that regardless of the shape of our population, the sampling distribution of the sample mean will be normal as the sample size increases.
Coefficient of Variation
To compare standard deviations between different populations or samples is difficult because the standard deviation depends on units of measure. The coefficient of variation expresses the standard deviation as a percentage of the sample or population mean. It is a unitless measure.
[latex]\boxed{6.8}[/latex] Coefficient of Variation (Population)
[latex]\begin{align*}{\color{red}{CV}}=\frac{{\color{blue}{\sigma}}}{{\color{green}{\mu}}}\times 100\end{align*}[/latex]
[latex]\boxed{6.9}[/latex] Coefficient of Variation (Sample)
[latex]\begin{align*}{\color{red}{CV}}=\frac{{\color{blue}{s}}}{{\color{green}{\bar{x}}}}\times 100\end{align*}[/latex]
[latex]{\color{red}{CV}}\text{ is the coefficient of variation.}[/latex]
[latex]{\color{blue}{\sigma}}\text{ and }{\color{blue}{s}}\text{ are the population and sample standard deviations, calculated by formulas }6.5\text{ and }6.6\text{ respectively.}[/latex]
[latex]{\color{green}{\mu}}\text{ and }{\color{green}{\bar{x}}}\text{ are the population and sample means, calculated by formulas }6.1\text{ and }6.2\text{ respectively.}[/latex]
Example 6.2.4
Fisheries biologists were studying the length and weight of Pacific salmon. They took a random sample and computed the mean and standard deviation for length and weight (given below). While the standard deviations are similar, the differences in units between lengths and weights make it difficult to compare the variability. Computing the coefficient of variation for each variable allows the biologists to determine which variable has the greater standard deviation.
| Sample Mean | Sample Standard Deviation | |
| Length | [latex]63[/latex] cm | [latex]19.97[/latex] cm |
| Weight | [latex]37.6[/latex] kg | [latex]19.39[/latex] kg |
| [latex]\begin{align*}CV_L=\frac{19.97}{53.0}\times 100=31.5\%\end{align*}[/latex] | [latex]\begin{align*}CV_W=\frac{19.39}{37.6}\times 100=51.6\%\end{align*}[/latex] |
There is greater variability in Pacific salmon weight compared to length.
Variability
Variability is described in many different ways. Standard deviation measures point-to-point variability within a sample, i.e., variation among individual sampling units. Coefficient of variation also measures point to point variability but on a relative basis (relative to the mean), and is not influenced by measurement units. Standard error measures the sample-to-sample variability, i.e. variation among repeated samples in the sampling process. Typically, we only have one sample and standard error allows us to quantify the uncertainty in our sampling process.
Basic Statistics Example using Excel and Minitab Software
Consider the following tally from [latex]11[/latex] sample plots on Heiburg Forest, where [latex]X_i[/latex] is the number of downed logs per acre. Compute basic statistics for the sample plots.
| ID | [latex]X_i[/latex] | [latex]X_i^2[/latex] | [latex](X_i-\bar{X})[/latex] | [latex](X_i-\bar{X})^2[/latex] | Order |
|---|---|---|---|---|---|
| [latex]1[/latex] | [latex]25[/latex] | [latex]625[/latex] | [latex]-7.27[/latex] | [latex]52.8529[/latex] | [latex]4[/latex] |
| [latex]2[/latex] | [latex]35[/latex] | [latex]1225[/latex] | [latex]2.73[/latex] | [latex]7.4529[/latex] | [latex]6[/latex] |
| [latex]3[/latex] | [latex]55[/latex] | [latex]3025[/latex] | [latex]22.73[/latex] | [latex]516.6529[/latex] | [latex]10[/latex] |
| [latex]4[/latex] | [latex]15[/latex] | [latex]225[/latex] | [latex]-17.25[/latex] | [latex]298.2529[/latex] | [latex]2[/latex] |
| [latex]5[/latex] | [latex]40[/latex] | [latex]1600[/latex] | [latex]7.73[/latex] | [latex]59.7529[/latex] | [latex]8[/latex] |
| [latex]6[/latex] | [latex]25[/latex] | [latex]625[/latex] | [latex]-7.27[/latex] | [latex]52.8529[/latex] | [latex]5[/latex] |
| [latex]7[/latex] | [latex]55[/latex] | [latex]3025[/latex] | [latex]22.73[/latex] | [latex]516.6529[/latex] | [latex]11[/latex] |
| [latex]8[/latex] | [latex]35[/latex] | [latex]1225[/latex] | [latex]2.73[/latex] | [latex]7.4529[/latex] | [latex]7[/latex] |
| [latex]9[/latex] | [latex]45[/latex] | [latex]2025[/latex] | [latex]12.73[/latex] | [latex]162.0529[/latex] | [latex]9[/latex] |
| [latex]10[/latex] | [latex]5[/latex] | [latex]25[/latex] | [latex]-27.27[/latex] | [latex]743.6529[/latex] | [latex]1[/latex] |
| [latex]11[/latex] | [latex]20[/latex] | [latex]400[/latex] | [latex]-12.27[/latex] | [latex]150.1819[/latex] | [latex]3[/latex] |
| Sum | [latex]355[/latex] | [latex]14025[/latex] | [latex]0.0[/latex] | [latex]2568.1519[/latex] | |
| [latex]\sum\limits_{i=1}^nX_i[/latex] | [latex]\sum\limits_{i=1}^nX_i^2[/latex] | [latex]\sum\limits_{i=1}^n(X_i-\bar{X})[/latex] | [latex]\sum\limits_{i=1}^n(X_i-\bar{X})^2[/latex] |
-
Sample mean:
[latex]\begin{align*}\bar{X}=\frac{\sum\limits_{i=1}^nX_i}{n}=\frac{355}{11}=32.27\end{align*}[/latex]
- Median = [latex]35[/latex]
-
Variance:
[latex]\begin{align*}S^2&=\frac{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)^2}{n-1}=\frac{2568.1519}{11-1}=256.82\\[1.5ex]&=\frac{\sum\limits_{i=1}^nX_i^2-\frac{\left(\sum\limits_{i=1}^nX_i\right)^2}{n}}{n-1}=\frac{14025-\frac{\left(355\right)^2}{11}}{11-1}=256.82\end{align*}[/latex]
-
Standard Deviation:
[latex]S=\sqrt{S^2}=\sqrt{256.82}=16.0256[/latex]
- Range: [latex]55 - 5 = 50[/latex]
-
Coefficient of variation:
[latex]\begin{align*}CV=\frac{S}{X}\cdot 100=\frac{16.0256}{32.27}\cdot 100=49.66\%\end{align*}[/latex]
-
Standard Error of the Mean:
[latex]\begin{align*}S_{\bar{X}}&=\sqrt{\frac{S^2}{n}}=\sqrt{\frac{256.82}{11}}=4.8319\\[1.5ex]&=\frac{S}{\sqrt{n}}=\frac{16.0256}{\sqrt{11}}=4.8319\end{align*}[/latex]
Attribution
"Chapter 1: Descriptive Statistics and the Normal Distribution" from Natural Resources Biometrics by Diane Kiernan is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

