2.2 Future Value of Annuities
Learning Objectives
- Calculate the future value of an ordinary annuity
- Calculate the future value of an annuity due
Formula & Symbol Hub
Symbols Used
- [latex]FV[/latex] = Future value or maturity value
- [latex]PV[/latex] = Present value of principal
- [latex]PMT[/latex] = Annuity payment amount
- [latex]I/Y[/latex] = Nominal interest rate
- [latex]P/Y[/latex] = Number of payments per year or payment frequency
- [latex]C/Y[/latex] = Number of compounds per year or compounding frequency
- [latex]n[/latex] or [latex]N[/latex] = Total number of annuity payments
Formulas Used
-
Formula 2.1 - Total Number of Payments (Annuity)
[latex]n=P/Y \times t[/latex]
-
Formula 2.2 - Future Value of Ordinary Annuity
[latex]FV=PMT \times \left[\frac{(1+i_2)^n-1}{i_2}\right][/latex]
-
Formula 2.3 - Future Value of Annuity Due
[latex]FV=PMT \times (1+i_2) \times \left[\frac{(1+i_2)^n-1}{i_2}\right][/latex]
Introduction
The future value of any annuity equals the sum of the future values for all of the annuity payments when they are moved to the end of the last payment interval. For example, assume you will make [latex]\$1,000[/latex] contributions at the end of every year for the next three years to an investment earning [latex]10\%[/latex] compounded annually. To find out how much money you have in your investment after the three years, you would apply the fundamental concept of the time value of money to move each payment amount to the future date (the focal date) and sum the values at the focal date to arrive at the future value.
Although you could use this technique to solve all future value of an annuity situations, the computations become increasingly cumbersome as the number of payments increases. In the above example, what if the person made quarterly contributions of [latex]\$250[/latex] for three years? That is [latex]12[/latex] payments over three years, resulting in [latex]11[/latex] separate future value calculations. Or if they made monthly payments, the [latex]36[/latex] payments over three years would result in [latex]35[/latex] separate future value calculations! Clearly, solving this would be tedious and time consuming—not to mention prone to error.
[latex]\boxed{2.2}[/latex] Future Value of Ordinary Annuities
[latex]{\color{red}{FV}}\;\text{is the Future Value of the Annuity:}[/latex] the future value is the sum of the future value of all of the annuity payments at the end of the last payment interval.
[latex]{\color{blue}{PMT}}\;\text{is the Annuity Payment:}[/latex] the amount of money that is invested or paid after each payment interval.
[latex]{\color{green}{i_2}}\;\text{is the Periodic Interest Rate:}[/latex] for the interest rate whose compounding frequency matches the payment frequency. If the annuity is a simple annuity, the compounding frequency and the payment frequency are equal and the given interest rate can be used to calculate the periodic interest rate. If the annuity is a general annuity, the compounding frequency and the payment frequency are different and an interest conversion must be done first to find the equivalent interest rate with the compounding frequency equal to the payment frequency.
[latex]{\color{purple}{n}}\;\text{is the Total Number of Payments made during the Annuity:}[/latex] [latex]n=P/Y \times t[/latex] where [latex]P/Y[/latex] is the payment frequency and [latex]t[/latex] is the time in years.
For investment annuities, the amount of interest ([latex]I[/latex]) earned by the annuity is
[latex]\displaystyle{I=FV- n \times PMT}[/latex]
Key Takeaways
In a simple annuity, the payment frequency and the compounding frequency are equal ([latex]P/Y=C/Y[/latex]). In this situation the periodic interest rate [latex]i_2=\frac{j}{m}[/latex] where [latex]j[/latex] is the nominal interest rate given in the question and [latex]m[/latex] is the compounding frequency (and the payment frequency).
In a general annuity, the payment frequency and the compounding frequency are not equal ([latex]P/Y \neq C/Y[/latex]). In this situation, the given interest rate must first be converted to the equivalent interest rate where the new compounding frequency equals the payment frequency. Using the equivalent interest rate, calculate the periodic interest rate [latex]i_2[/latex].
Example 2.2.1
A financial adviser is reviewing one of her client's accounts. The client has been investing [latex]\$1,000[/latex] at the end of every quarter for the past [latex]11[/latex] years in a fund that has averaged [latex]7.3\%[/latex] compounded quarterly. How much money does the client have in his account today? How much interest did the client earn?
Solution
The timeline shows the client's account.

Step 1: The given information is
The payments are at the end of the payment intervals, and both the compounding frequency and the payment frequency are the same (both quarterly). This is an ordinary simple annuity. Because this is a simple annuity, an interest rate conversion is not required.
[latex]\begin{eqnarray*} PMT & = & \$1,000 \\ P/Y & = & 4 \\ I/Y & = & 7.3\% \\ C/Y & = & 4 \\ t & = & 11 \mbox{ years} \end{eqnarray*}[/latex]
Step 2: Calculate the periodic interest rate.
[latex]\begin{eqnarray*} i_2 & = & \frac{I/Y}{C/Y} \\ & = & \frac{7.3\%}{4}\\ & = & 1.825\%\end{eqnarray*}[/latex]
Step 3: Calculate the number of payments.
[latex]\begin{eqnarray*} n & = & P/Y \times t \\ & = & 4 \times 11 \\ & = & 44 \end{eqnarray*}[/latex]
Step 4: Calculate the future value.
[latex]\begin{eqnarray*} FV & = & PMT \times \left[\frac{(1+i_2)^n-1}{i_2}\right] \\ & = & 1,000 \times \left[ \frac{(1+0.01825)^{44}-1}{0.01825}\right] \\ & = & \$66,637.03 \end{eqnarray*}[/latex]
Step 5: Calculate the interest earned.
[latex]\begin{eqnarray*} I & = & FV-n \times PMT \\ & = & 66,637.03-44 \times 1,000 \\ & = & \$22,637.03 \end{eqnarray*}[/latex]
Step 6: Write as a statement.
After [latex]11[/latex] years, the client has [latex]\$66,637.03[/latex] in the account and has earned [latex]\$22,637.03[/latex] in interest.
Using a Financial Calculator
The above example was a fairly straightforward annuity question. But even this simple example, which did not require an interest conversion, is cumbersome, and time-consuming, to solve using the formula. A financial calculator can quickly solve annuity problems, with the added bonus of not requiring an interest conversion in situations where the payment frequency and compounding frequency are not equal.
Using the TI BAII Plus Calculator to Find the Future Value for Ordinary Annuities
The time value of money buttons are located in the [latex]TVM[/latex] row (the third row from the top) of the calculator. The five buttons located on the third row of the calculator are five of the seven variables required for time value of money calculations. This row’s buttons are different in colour from the rest of the buttons on the keypad. The other two variables are in a secondary menu above the [latex]I/Y[/latex] key and are accessed by pressing 2nd I/Y.

Image Description
The image is of a black Texas Instruments BA II Plus financial calculator. The calculator has a large LCD screen at the top which is displaying the number "0.". Below the screen, there is a keypad with numerous buttons divided into several rows. The buttons provide various financial calculations and standard calculator functions.
There are labels indicating two key sections of the calculator:
- The Frequency Functions are indicated in blue as the secondary functions of the third row of buttons from the top:
- xP/Y
- P/Y
- AMORT
- BGN
- CLR TVM
- Time Value of Money Buttons are indicated in red as the primary functions of the third row of buttons from the top:
- N
- I/Y
- PV
- PMT
- FV
Altogether, there are seven variables required to complete time value of money calculations. Note that [latex]P/Y[/latex] and [latex]C/Y[/latex] are not main button keys in the [latex]TVM[/latex] row. The P/Y and C/Y variables are located in the secondary function accessed by pressing 2nd I/Y.
| Variable | Meaning |
| [latex]N[/latex] | Total number of payments. This is the same value as [latex]n[/latex] in the future value formula. [latex]N=P/Y \times \mbox{time in years}[/latex] |
| [latex]I/Y[/latex] | Interest rate per year (i.e. the nominal interest rate). The interest rate is entered in percent form (without the [latex]\%[/latex] sign). For example, [latex]5\%[/latex] is entered as [latex]5[/latex] |
| [latex]PV[/latex] | Present value or principal |
| [latex]PMT[/latex] | Periodic annuity payment |
| [latex]FV[/latex] | Future value or maturity value |
| [latex]P/Y[/latex] | Payment frequency |
| [latex]C/Y[/latex] | Compounding frequency |
To enter values into the calculator:
- For the main button [latex]null[/latex] keys in the [latex]TVM[/latex] row (i.e. [latex]N[/latex], [latex]I/Y[/latex], [latex]PV[/latex], [latex]PMT[/latex], [latex]FV[/latex]), enter the number first and then press the corresponding button.
- For [latex]P/Y[/latex]and [latex]C/Y[/latex], press 2nd I/Y. At the [latex]P/Y[/latex] screen, enter the value for [latex]P/Y[/latex] and then press ENTER. Press the down arrow to access the [latex]C/Y[/latex] screen. At the [latex]C/Y[/latex] screen, enter the value for [latex]C/Y[/latex] and then press ENTER. Press 2nd QUIT (the [latex]CPT[/latex] button) to exit the menu.
After all of the known quantities are loaded into the calculator, press [latex]CPT[/latex] and then [latex]FV[/latex] to solve for the future value.
Notes
- Be sure to enter [latex]PV[/latex], [latex]FV[/latex], and [latex]PMT[/latex] with the correct cash flow sign convention. When you invest, [latex]PMT[/latex] has the same sign as the [latex]PV[/latex] (both negative). When you borrow, [latex]PMT[/latex] has the opposite sign of [latex]PV[/latex] ([latex]PMT[/latex] is negative and [latex]PV[/latex] is positive).
- Because you can enter [latex]P/Y[/latex] and [latex]C/Y[/latex], there is no need to do an interest conversion for a general annuity. You simply have to tell the calculator the [latex]P/Y[/latex] and [latex]C/Y[/latex] given in the question, and the calculator will handle any interest conversion internally.
- If there is no money in the account or investment to start, then [latex]PV=0[/latex].
Video: Ordinary Annuity Calculations (PV, PMT, FV) by Joshua Emmanuel [4:31] (Transcript Available).
Example 2.2.2
A financial adviser is reviewing one of her client's accounts. The client has been investing [latex]\$1,000[/latex] at the end of every quarter for the past [latex]11[/latex] years in a fund that has averaged [latex]7.3\%[/latex] compounded quarterly. How much money does the client have in his account today?
Solution

The timeline shows the client's account.
| PMT Setting | END |
| [latex]N[/latex] | [latex]4 \times 11=44[/latex] |
| [latex]PV[/latex] | [latex]0[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-1,000[/latex] |
| [latex]I/Y[/latex] | [latex]7.3[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]FV=\$66,637.03[/latex]
After 11 years, the client as [latex]\$66,637.03[/latex] in the account.
Try It
1) You are a financial adviser. Your client is thinking of investing [latex]\$600[/latex] at the end of every six months for the next six years with the invested funds earning [latex]6.4\%[/latex] compounded semi-annually. Your client wants to know how much money she will have after six years. What do you tell your client?
Solution
| PMT Setting | END |
| [latex]N[/latex] | [latex]2 \times 12=24[/latex] |
| [latex]PV[/latex] | [latex]0[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-600[/latex] |
| [latex]I/Y[/latex] | [latex]6.4[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV=\$8,612.62[/latex]
Example 2.2.4
A savings annuity already contains [latex]\$10,000[/latex]. If an additional [latex]\$250[/latex] is invested at the end of every month at [latex]9\%[/latex] compounded semi-annually for a term of [latex]20[/latex] years, what will be the maturity value of the investment?
Solution
The timeline is shown below.

PMT SettingEND[latex]N[/latex][latex]12 \times 20=240[/latex][latex]PV[/latex][latex]-10,000[/latex][latex]FV[/latex]?[latex]PMT[/latex][latex]-250[/latex][latex]I/Y[/latex][latex]9[/latex][latex]P/Y[/latex][latex]12[/latex][latex]C/Y[/latex][latex]2[/latex]
[latex]FV=\$221,693.59[/latex]
The savings annuity will have a balance of [latex]\$221,693.59[/latex] after the [latex]20[/latex] years.
Try It
2) McDonald's major distribution partner, The Martin-Brower Company, needs at least [latex]\$1,000,000[/latex] to build a new warehouse in Medicine Hat two years from today. To date, it has invested [latex]\$500,000[/latex]. If it continues to invest [latex]\$50,000[/latex] at the end of every quarter into a fund earning [latex]6\%[/latex] quarterly, will it have enough money to build the warehouse two years from now?
Solution
| PMT Setting | END |
| [latex]N[/latex] | [latex]4 \times 2=8[/latex] |
| [latex]PV[/latex] | [latex]-500,000[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-50,000[/latex] |
| [latex]I/Y[/latex] | [latex]6[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]FV=\$984,888.25[/latex]
The fund is [latex]\$15,111.75[/latex] short of the $1 million target.
If any of the variables, including [latex]I/Y[/latex], [latex]C/Y[/latex], [latex]PMT[/latex], or [latex]P/Y[/latex] change between the starting point and ending point of the annuity, or if any additional single payment deposit or withdrawal is made, a new time segment is created and must be treated separately. In such cases, there will be multiple time segments that require you to work from left to right through the timeline in order to find the future value at the end of the annuity. The future value at the end of one time segment becomes the present value in the next time segment.
Example 2.2.5
Genevieve has decided to start saving up for a vacation in two years, when she graduates from university. She already has [latex]\$1,000[/latex] saved today. For the first year, she plans on making end-of-month contributions of [latex]\$300[/latex] and then switching to end-of-quarter contributions of [latex]\$1,000[/latex] in the second year. If the account can earn [latex]5\%[/latex] compounded semi-annually in the first year and [latex]6\%[/latex] compounded quarterly in the second year, how much money will she have saved when she graduates?
Solution
The timeline for her vacation saving appears below.
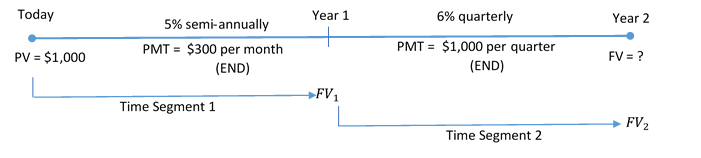
Step 1: Find the future value at the end of the first segment.
| PMT Setting | END |
| [latex]N[/latex] | [latex]12 \times 1=12[/latex] |
| [latex]PV[/latex] | [latex]-1,000[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-300[/latex] |
| [latex]I/Y[/latex] | [latex]5[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV_1=\$4,733.411...[/latex]
Step 2: Calculate the future value at the end of the second segment.
The future value from the first segment becomes the present value for the second segment: [latex]FV_1=\$4,733.411...=PV_2[/latex].
| PMT Setting | END |
| [latex]N[/latex] | [latex]4 \times 1=4[/latex] |
| [latex]PV[/latex] | [latex]-4,733.411...[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-1,000[/latex] |
| [latex]I/Y[/latex] | [latex]6[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]4[/latex] |
[latex]FV_2=\$9,114.77[/latex]
Step 3: Write as a statement.
When Genevieve graduates she will have saved [latex]\$9,114.77[/latex] toward her vacation.
Try It
3) Carlyle plans to make month-end contributions of [latex]\$400[/latex] to his RRSP from age 20 to age 40. From age 40 to age 65, he plans to make no further contributions to his RRSP. The RRSP can earn [latex]9\%[/latex] compounded annually from age 20 to age 60, and then [latex]5\%[/latex] compounded annually from age 60 to age 65. Under this plan, what is the maturity value of his RRSP when he turns 65?
Solution
| PMT Setting | END | END | END |
| [latex]N[/latex] | [latex]240[/latex] | [latex]20[/latex] | [latex]5[/latex] |
| [latex]PV[/latex] | [latex]0[/latex] | [latex]-255,540.68...[/latex] | [latex]1,432,254.94...[/latex] |
| [latex]FV[/latex] | [latex]\color{blue}{255,540.68...}[/latex] | [latex]\color{blue}{1,432,254.94...}[/latex] | [latex]\color{blue}{1,827,832.95}[/latex] |
| [latex]PMT[/latex] | [latex]-400[/latex] | [latex]0[/latex] | [latex]0[/latex] |
| [latex]I/Y[/latex] | [latex]9[/latex] | [latex]9[/latex] | [latex]5[/latex] |
| [latex]P/Y[/latex] | [latex]12[/latex] | [latex]1[/latex] | [latex]1[/latex] |
| [latex]C/Y[/latex] | [latex]1[/latex] | [latex]1[/latex] | [latex]1[/latex] |
[latex]FV=\$1,827,832.95[/latex]
[latex]\boxed{2.3}[/latex] Future Value of Annuities Due
[latex]{\color{red}{FV}}\;\text{is the future value of the annuity:}[/latex] the future value is the sum of the future value of all of the annuity payments at the end of the last payment interval.
[latex]{\color{blue}{PMT}}\;\text{is the annuity payment:}[/latex] the amount of money that is invested or paid after each payment interval.
[latex]{\color{green}{i_2}}\;\text{is the periodic interest rate:}[/latex] for the interest rate whose compounding frequency matches the payment frequency. If the annuity is a simple annuity, the compounding frequency and the payment frequency are equal and the given interest rate can be used to calculate the periodic interest rate. If the annuity is a general annuity, the compounding frequency and the payment frequency are different and an interest conversion must be done first to find the equivalent interest rate with the compounding frequency equal to the payment frequency.
[latex]{\color{purple}{n}}\;\text{is the total number of payments made during the annuity:}[/latex] [latex]n=P/Y \times t[/latex] where [latex]P/Y[/latex] is the payment frequency and [latex]t[/latex] is the time in years.
For investment annuities, the amount of interest ([latex]I[/latex]) earned by the annuity is
[latex]\displaystyle{I=FV- n \times PMT}[/latex]
Key Takeaways
The steps required to solve the future value of an annuity due are identical to those you use for an ordinary annuity except you use the formula for the future value of an annuity due.
If the payment setting is NOT specified in the question, it is assumed that the payments come at the end of the interval.
Using the TI BAII Plus Calculator to Find the Future Value for Annuities Due
To adapt your calculator to an annuity due, you must toggle the payment setting from END to BGN. The calculator default is END, which is the ordinary annuity. The payment setting is found on the second shelf above the [latex]PMT[/latex] key (because it is related to the [latex]PMT[/latex]!).

Image Description
The image depicts a Texas Instruments BA II Plus financial calculator with certain buttons and display elements highlighted and annotated for instructional purposes.
- Top of calculator: The display screen shows "BGN", "SET", and "END". An annotation points to "BGN" indicating that it will appear when in annuity due mode.
- Left side of keypad: The button labeled "ENTER" is highlighted, and an annotation points out that it is used to toggle the setting.
- Middle of keypad: The button labeled "CPT" is highlighted, with an annotation indicating that it is used to exit the window.
- Right side of keypad: The button labeled "PMT" is highlighted, with an annotation indicating it is the payment timing button.
To change the payment setting, complete the following sequence.
- Press 2nd BGN (the [latex]PMT[/latex] button).
- Press 2nd SET (the ENTER button).
- Press 2nd QUIT (the [latex]CPT[/latex] button).
When the calculator is in annuity due mode, a tiny BGN appears in the upper right-hand corner of your calculator. To return the calculator to ordinary mode, repeat the above keystrokes. When the calculator is in ordinary annuity mode there is nothing in the upper right-hand corner.
To calculate the future value of annuity due, make sure the calculator is in BGN mode. Then enter the values of [latex]N[/latex], [latex]I/Y[/latex], [latex]PV[/latex], [latex]PMT[/latex], [latex]P/Y[/latex] and [latex]C/Y[/latex] into the [latex]TVM[/latex] money keys on the calculator and compute FV.
Annuity Due Calculations Using the BAII Plus by Joshua Emmanuel [2:51] (transcript available).
Example 2.2.6
The Set for Life instant scratch n' win ticket offers players a chance to win [latex]\$1,000[/latex] per week for the next [latex]25[/latex] years starting immediately upon validation. If a winner was to invest all of his money into an account earning [latex]5\%[/latex] compounded annually, how much money would he have at the end of his [latex]25[/latex]-year term? Assume each year has exactly [latex]52[/latex] weeks.
Solution
The timeline for the lottery savings is below.

The payments start immediately, and the compounding period and payment intervals are different. Therefore, this a general annuity due.
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]52 \times 25=1,300[/latex] |
| [latex]PV[/latex] | [latex]0[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-1,000[/latex] |
| [latex]I/Y[/latex] | [latex]5[/latex] |
| [latex]P/Y[/latex] | [latex]52[/latex] |
| [latex]C/Y[/latex] | [latex]1[/latex] |
[latex]FV=\$2,544,543.22[/latex]
If the winner was to invest all of his lottery prize money, he would have [latex]\$2,544,543.22[/latex] after [latex]25[/latex] years.
Try It
4) The Saskatchewan Roughriders started a rainy-day savings fund three-and-a-half years ago to help pay for stadium improvements. At the beginning of every quarter the team deposited [latex]\$20,000[/latex] into the fund, which has been earning [latex]4.85\%[/latex] compounded semi-annually. How much money is in the fund today? How much interest did the fund earn?
Solution
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]4 \times 3.5=14[/latex] |
| [latex]PV[/latex] | [latex]0[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-20,000[/latex] |
| [latex]I/Y[/latex] | [latex]4.85[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]2[/latex] |
[latex]FV=\$306,680.93[/latex]
[latex]\begin{eqnarray*} I & = & FV-n \times PMT \\ & = & 306,680.93-14 \times 20,000 \\ & = & \$26,680.93 \end{eqnarray*}[/latex]
Example 2.2.7
When Roberto's son was born, Roberto started making payments of [latex]\$1,000[/latex] at the beginning of every six months to a trust fund earning [latex]5.75\%[/latex] compounded monthly. After five years, he changed his contributions and started depositing [latex]\$500[/latex] at the beginning of every quarter. How much money will be in his son's trust fund when his son turns [latex]18[/latex]?
Solution
The timeline for the trust fund is shown below.
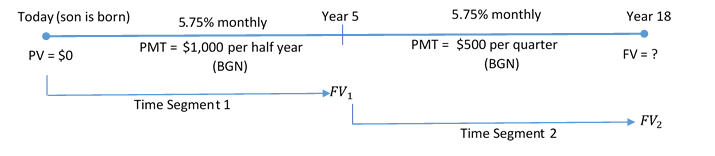
Step 1: Find the future value at the end of the first segment.
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]2 \times 5=10[/latex] |
| [latex]PV[/latex] | [latex]0[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-1,000[/latex] |
| [latex]I/Y[/latex] | [latex]5.75[/latex] |
| [latex]P/Y[/latex] | [latex]2[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]FV_1=\$11,748.474...[/latex]
Step 2: Calculate the future value at the end of the second segment.
The future value from the first segment becomes the present value for the second segment: [latex]FV_1=\$11,748.474...=PV_2[/latex].
| PMT Setting | BGN |
| [latex]N[/latex] | [latex]4 \times 13=52[/latex] |
| [latex]PV[/latex] | [latex]-11,748.474...[/latex] |
| [latex]FV[/latex] | ? |
| [latex]PMT[/latex] | [latex]-500[/latex] |
| [latex]I/Y[/latex] | [latex]5.75[/latex] |
| [latex]P/Y[/latex] | [latex]4[/latex] |
| [latex]C/Y[/latex] | [latex]12[/latex] |
[latex]FV_2=\$63,672.39[/latex]
Step 3: Write as a statement.
When Roberto’s son turns [latex]18[/latex], the trust fund will have a balance of [latex]\$63,672.39[/latex].
Section 2.2 Exercises
- You invest [latex]\$2,000[/latex] at the beginning of every quarter into a savings account earning [latex]7\%[/latex] compounded quarterly. How much money is in your account in [latex]10[/latex] years? How much interest did the account earn?
Solution
[latex]\$116,471.46, \$36,471.46[/latex]
- For [latex]20[/latex] years, Joan deposits [latex]\$375[/latex] every quarter into her RRSP. If the RRSP earns [latex]9\%[/latex] compounded monthly, how much money does Joan have in her RRSP at the end of the [latex]20[/latex] years?
Solution
[latex]\$250,457.58[/latex]
- Your savings account currently has [latex]\$15,000[/latex]. For the next [latex]30[/latex] years, you plan to deposit [latex]\$3,000[/latex] at the end of every year. If the account earns [latex]5.6\%[/latex] compounded quarterly, how much money will you have in the account at the end of the [latex]30[/latex] years?
Solution
[latex]\$305,305.23[/latex]
- Jesse's RRSP has a balance of [latex]\$38,000[/latex]. Over the next [latex]8[/latex] years, Jesse will invest [latex]\$1,500[/latex] at the beginning of every month. The RRSP earns [latex]8\%[/latex] compounded semi-annually. How much money will be in Jesse's RRSP in [latex]8[/latex] years?
Solution
[latex]\$272,152.25[/latex]
- You open a savings account to save money for a down payment on a house. You deposit [latex]\$1,000[/latex] every quarter for [latex]10[/latex] years. For the first four years, the account earns [latex]6\%[/latex] compounded annually. For the last six years, the account earns [latex]7\%[/latex] compounded semi-annually. How much money can you save for your down payment? How much interest did you earn?
Solution
[latex]\$56,486.35, \$16,486.35[/latex]
- Phil invests [latex]\$100[/latex] at the beginning of every month into an RRSP for [latex]10[/latex] years. For the first [latex]6.5[/latex] years, the RRSP earns [latex]12\%[/latex] compounded quarterly. For the last [latex]3.5[/latex] years, the RRSP earns [latex]11\%[/latex] compounded semi-annually. How much money is in Phil's RRSP at the end of the [latex]10[/latex] years? How much interest did Phil's RRSP earn?
Solution
[latex]\$22,278.17, \$10,278.17[/latex]
- Nikola is currently [latex]47[/latex] years old and planning to retire at age [latex]60[/latex]. She has already saved [latex]\$220,000[/latex] in her RRSP. If she continues to contribute [latex]\$200[/latex] at the beginning of every month, how much money will be in her RRSP at retirement if it can earn [latex]8.1\%[/latex] compounded monthly? No deposit is made the day she turns [latex]60[/latex].
Solution
[latex]\$683,712.33[/latex]
- The human resource department helps employees save by taking preauthorized RRSP deductions from employee paycheques and putting them into an investment. For the first five years, Margaret has had [latex]\$50[/latex] deducted at the beginning of every biweekly pay period. Then for the next five years, she increased the deduction to [latex]\$75[/latex]. The company has been able to average [latex]8.85\%[/latex] compounded monthly for the first seven years, and then [latex]7.35\%[/latex] compounded monthly for the last three years. What amount has Margaret accumulated in her RRSP after [latex]10[/latex] years? Assume there are [latex]26[/latex] biweekly periods in a year.
Solution
[latex]\$24,035.26[/latex]
- Joshua is opening up a Builder GIC that allows him to make regular contributions to his GIC throughout the term. He will initially deposit [latex]\$10,000[/latex], then at the end of every month for the next five years he will make [latex]\$100[/latex] contributions to his GIC. The annually compounded interest rates on the GIC in each year are [latex]0.75\%, 1.5\%, 2.5\%, 4.5\%[/latex], and [latex]7.25\%[/latex]. What is the maturity value of his GIC?
Solution
[latex]\$18,452.55[/latex]
- How much more money would an individual who makes [latex]\$300[/latex] contributions to her RRSP at the beginning of the month have compared to another individual who makes [latex]\$300[/latex] contributions to his RRSP at the end of the month? Assume a term of [latex]30[/latex] years and that both RRSPs earn [latex]9\%[/latex] annually.
Solution
[latex]\$3680.30[/latex]
- Assume a [latex]10[/latex]-year ordinary annuity earning [latex]10\%[/latex] compounded annually.
- If [latex]\$5,000[/latex] is deposited annually, what is the maturity value?
- What is the maturity value if the deposits are doubled to [latex]\$10,000[/latex]? Compared to (a), what is the relationship between the size of the deposit and the maturity value, all other conditions being held equal?
- What is the maturity value if the [latex]\$5,000[/latex] deposits are made semi-annually? Compared to (b), what is the relationship between the frequency of payments and the maturity value, all other conditions being held equal?
Solution
a. [latex]\$79,687.12[/latex], b. [latex]\$159,377.24[/latex], c. [latex]\$163,263.68[/latex]
Attribution
"2.2 Future Value of Annuities" from Financial Math - Math 1175 by Margaret Dancy is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

