Derivative as a Rate of Change

Introduction

Precalculus Idea: Slope and Rate of Change

The slope of a line measures how fast a line rises or falls as we move from left to right along the line. It measures the rate of change of the y-coordinate with respect to changes in the x-coordinate. If the line represents the distance traveled over time, for example, then its slope represents the velocity. In the figure, you can remind yourself of how we calculate slope using two points on the line:

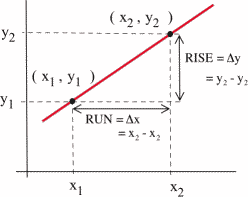
[latex]m=\text{Slope from \( P \) to \( Q \)}=\dfrac{\text{rise}}{\text{run}}=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{\Delta y}{\Delta x}[/latex]

We would like to be able to get that same sort of information (how fast the curve rises or falls, velocity from distance) even if the graph is not a straight line. But what happens if we try to find the slope of a curve, as in the figure below?

image

We need two points in order to determine the slope of a line. How can we find a slope of a curve, at just one point? The answer, as suggested in the figure, is to find the slope of the tangent line to the curve at that point. Most of us have an intuitive idea of what a tangent line is. Unfortunately, “tangent line” is hard to define precisely.

Definition (Secant Line)

A secant line is a line between two points on a curve

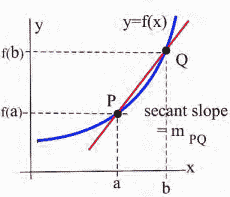
See the image below:

image

Can’t-quite-do-it-yet Definition (Tangent Line)

A tangent line is a line at one point on a curve… that does its best to be the curve at that point?

As you may be able to see in the image below, the closer the point <span id=”MathJax-Element-2-Frame” class=”mjx-chtml MathJax_CHTML” style=”margin: 0px;padding: 1px 0px;line-height: 0;text-indent: 0px;text-align: left;text-transform: none;font-style: normal;font-weight: 400;font-size: 18.54px;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;color: #000000;font-family: ‘Times New Roman’, Times, serif” role=”presentation” data-mathml=”

Q

“> is to the point <span id=”MathJax-Element-3-Frame” class=”mjx-chtml MathJax_CHTML” style=”margin: 0px;padding: 1px 0px;line-height: 0;text-indent: 0px;text-align: left;text-transform: none;font-style: normal;font-weight: 400;font-size: 18.54px;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;color: #000000;font-family: ‘Times New Roman’, Times, serif” role=”presentation” data-mathml=”

P

“>

P

, the closer the secant slope gets to the tangent slope. This will be key to finding the tangent slope, but first we need to more carefully define the idea of getting closer to.

image

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Mathematical Analysis for Business Copyright © 2021 by Ana Duff is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book