2.1 Limits and Continuity

Introduction

Precalculus Idea: Slope and Rate of Change

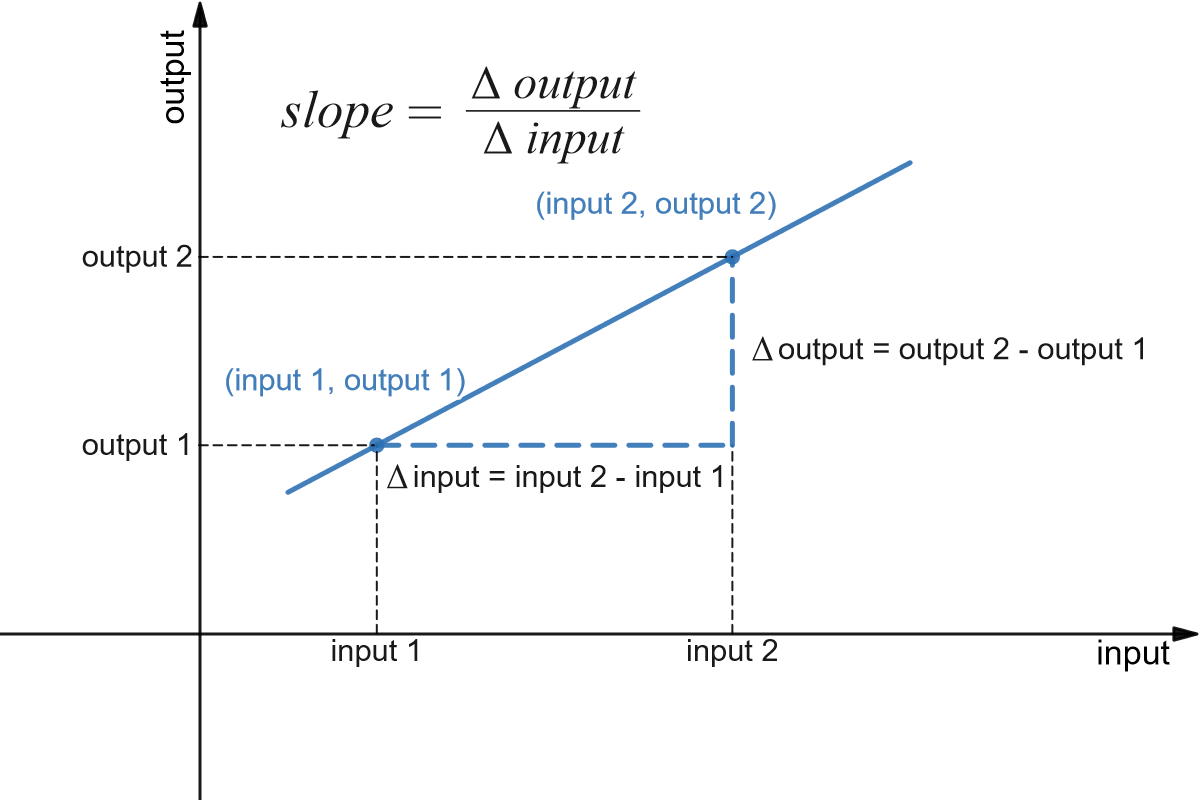
The slope of a line measures how fast a line rises or falls as we move from left to right along the line. It measures the rate of change of the y-coordinate with respect to changes in the x-coordinate. If the line represents the distance traveled over time, for example, then its slope represents the velocity. In the figure, you can remind yourself of how we calculate slope using two points on the line:
 

[latex]\text{slope between two points}=\dfrac{\Delta \text{output}}{\Delta \text{input}}=\dfrac{\text{output}_2-\text{output}_1}{\text{input}_2-\text{input}_1}[/latex]

We can also think of slope in contextual, not graph terms. It represents the rate of change in output in relation to the change in input. The value of slope will tell us whether the line connecting the two points is flat or going up or going down, and by how much over one horizontal unit. In the context of rate of change, this value will tell us how, and by how much, the output is changing with respect change in one unit of input.

So when we talk about slope, we are talking about slope between two points. Equivalently, when we talk about rate of change, we are talking about two input-output pairs and how the change from one to the other can be described. Therefore, we always need two pairs of input-output vales.

However, if you are walking up a hill, or walking down a hill and you stop, you’ll still think of being on “a steep slope” or “a gentle slope” even though the hill you are on is not a straight line. Note that when you are thinking about the slope at the point you are standing, this is not specific to a slope between two points on the hill. So where does that sense of slope on a hill come from? It comes from approximating the steepness (and the direction, as in up or down) by brain picking two imaginary points close to where you are standing and getting a rough estimate of slope. This concept, of being able to calculate slope at a single point, without a reference to some other specific point, is fundamentally behind the concept of “instantaneous rate of change”, which we will discuss throughout this chapter.

So, we would like to be able to get that same sort of information about slope (how fast the curve rises or falls, velocity from distance) even if the graph is not a straight line. But what happens if we try to find the slope of a curve, as in the figure below?
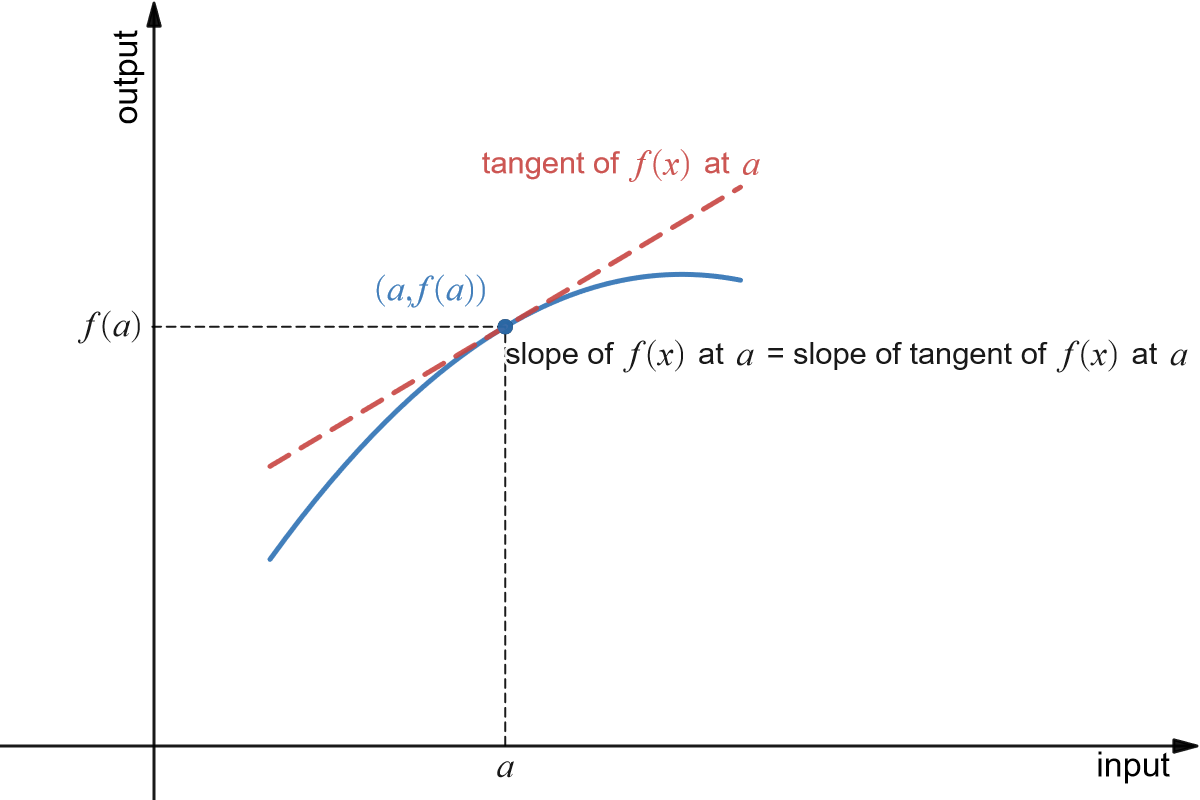Slope at point in terms of slope of tangent at pointSo if we need two points in order to determine the slope of a line, how can we find a slope of a curve at just one point? The answer, as suggested in the figure, is to find the slope of the tangent line to the curve at that point. Most of us have an intuitive idea of what a tangent line is. Unfortunately, “tangent line” is hard to define precisely.

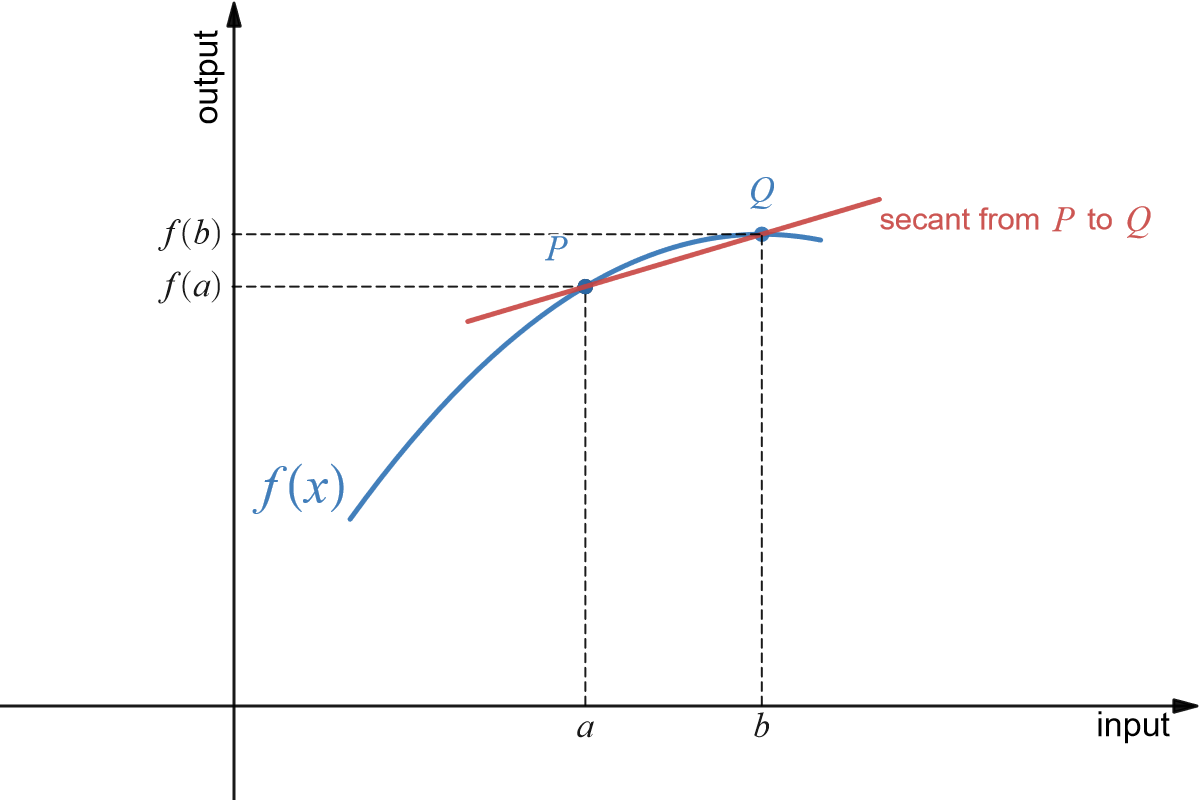
Definition (Secant Line)

A secant line is a line between two points on a curve.

Secant between two points on the graphCan’t-quite-do-it-yet Definition (Tangent Line)

A tangent line is a line at one point on a curve that does its best to be the curve at that point?

 

As you may be able to see in the image below, the closer the point [latex]Q[/latex] is to the point [latex]P[/latex], the closer the secant slope gets to the tangent slope. This will be key to finding the tangent slope, but first we need to more carefully define the idea of “getting closer to”.
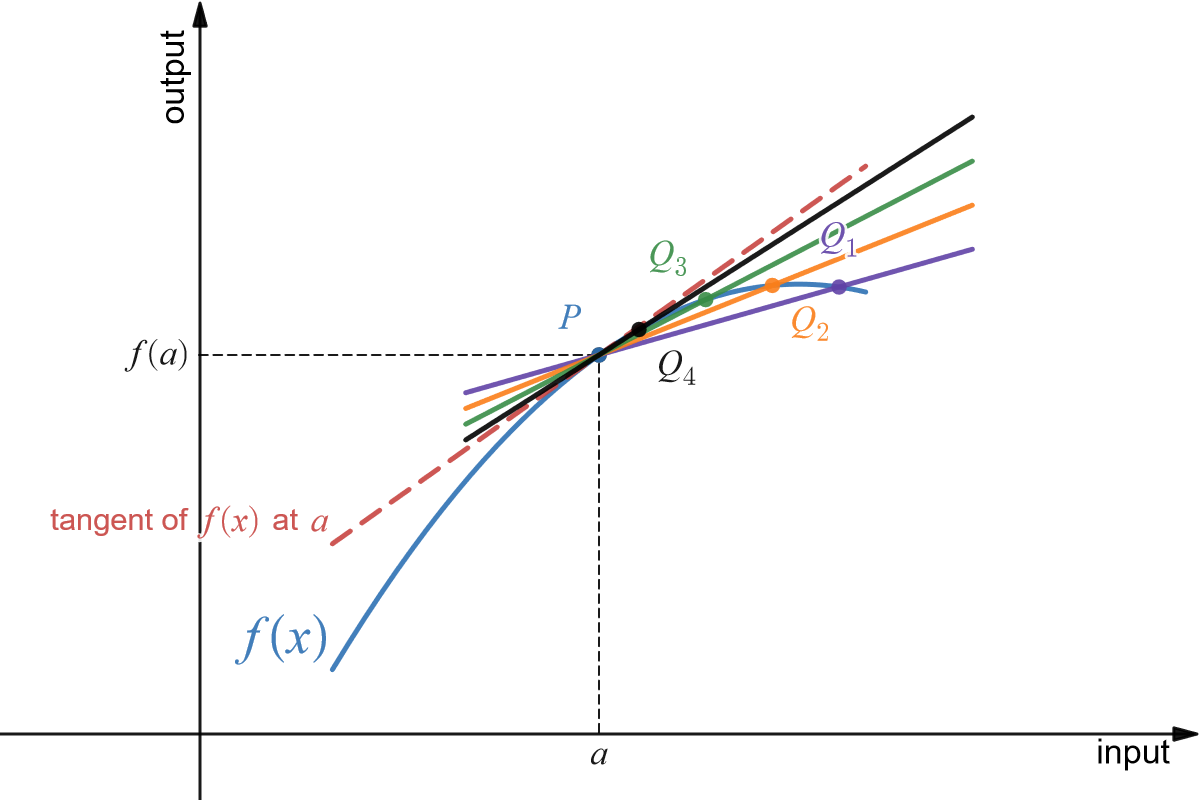
Sequence of secants towards the tangent

Section 2.1: Limits and Continuity

Limits

In the last section, we saw that as the interval over which we calculated got smaller, the secant slopes approached the tangent slope. The limit gives us better language with which to discuss the idea of “approaches.”
The limit of a function describes the behavior of the function when the variable is near, but does not equal, a specified number (see the figure below).
graph

Definition (Limit)

If the values of [latex]f(x)[/latex] get closer and closer, as close as we want, to one number [latex]L[/latex] as we take values of [latex]x[/latex] very close to (but not equal to) a number [latex]c[/latex], then we say ” the limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches [latex]c[/latex] is [latex]L[/latex] ” and we write \[\lim\limits_{x\to c} f(x)=L.\] The symbol “[latex]\to[/latex]” means “approaches” or, less formally, “gets very close to”.
(This definition of the limit isn’t stated as formally as it could be, but it is sufficient for our purposes in this course.)

 

Note:
  • [latex]f(c)[/latex] is a single number that describes the behavior (value) of [latex]f(x)[/latex] at the point [latex]x = c[/latex].
  • [latex]\lim\limits_{x\to c} f(x)[/latex] is a single number that describes the behavior of [latex]f(x)[/latex] near, but NOT at , the point [latex]x = c[/latex].
If we have a graph of the function near x = c, then it is usually easy to determine [latex]\lim\limits_{x\to c} f(x)[/latex].

Example 1

Use the graph of [latex]y = f(x)[/latex] in the figure below to determine the following limits:
  1. [latex]\lim\limits_{x\to 1} f(x)[/latex]
  2. [latex]\lim\limits_{x\to 2} f(x)[/latex]
  3. [latex]\lim\limits_{x\to 3} f(x)[/latex]
  4. [latex]\lim\limits_{x\to 4} f(x)[/latex]

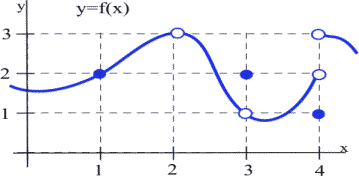
graph

  1. When [latex]x[/latex] is very close to 1, the values of [latex]f(x)[/latex] are very close to [latex]y = 2[/latex]. In this example, it happens that [latex]f(1) = 2[/latex], but that is irrelevant for the limit. The only thing that matters is what happens for [latex]x[/latex] close to 1 but [latex]x \neq 1[/latex].
  2. [latex]f(2)[/latex] is undefined, but we only care about the behavior of [latex]f(x)[/latex] for [latex]x[/latex] close to 2 but not equal to 2. When [latex]x[/latex] is close to 2, the values of [latex]f(x)[/latex] are close to 3. If we restrict [latex]x[/latex] close enough to 2, the values of [latex]y[/latex] will be as close to 3 as we want, so [latex]\lim\limits_{x\to 2} f(x) = 3[/latex].
  3. When [latex]x[/latex] is close to 3 (or “as [latex]x[/latex] approaches the value 3″), the values of [latex]f(x)[/latex] are close to 1 (or “approach the value 1”), so [latex]\lim\limits_{x\to 3} f(x) = 1[/latex]. For this limit it is completely irrelevant that [latex]f(3) = 2[/latex], We only care about what happens to [latex]f(x)[/latex] for [latex]x[/latex] close to and not equal to 3.
  4. This one is harder and we need to be careful. When [latex]x[/latex] is close to 4 and slightly less than 4 ([latex]x[/latex] is just to the left of 4 on the [latex]x[/latex]-axis), then the values of [latex]f(x)[/latex] are close to 2. But if [latex]x[/latex] is close to 4 and slightly larger than 4 then the values of [latex]f(x)[/latex] are close to 3. If we only know that [latex]x[/latex] is very close to 4, then we cannot say whether [latex]y = f(x)[/latex] will be close to 2 or close to 3–it depends on whether [latex]x[/latex] is on the right or the left side of 4. In this situation, the [latex]f(x)[/latex] values are not close to a single number so we say [latex]f(x)[/latex] does not exist. It is irrelevant that [latex]f(4) = 1[/latex]. The limit, as [latex]x[/latex] approaches 4, would still be undefined if [latex]f(4)[/latex] was 3 or 2 or anything else.

We can also explore limits using tables and using algebra: view video example.

(by Eric Bancroft, licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License)

 

Example 2

Find [latex]\lim\limits_{x\to 1} \dfrac{2x^2-x-1}{x-1}[/latex].

Answer:

You might try to evaluate at [latex]x = 1[/latex], but [latex]f(x)[/latex] is not defined at [latex]x = 1[/latex]. It is tempting, but incorrect , to conclude that this function does not have a limit as [latex]x[/latex] approaches 1.

Using tables: Trying some “test” values for x which get closer and closer to 1 from both the left and the right, we get
[latex]x[/latex] [latex]f(x)[/latex]
0.9 2.82
0.9998 2.9996
0.999994 2.999988
0.9999999 2.9999998
$latex  \to 1 $ $latex  \to 3 $
[latex]x[/latex] [latex]f(x)[/latex]
1.1 3.2
1.003 3.006
1.0001 3.0002
1.000007 3.000014
[latex]\to 1[/latex] [latex]\to 3[/latex]

The function [latex]f[/latex] is not defined at [latex]x = 1[/latex], but when [latex]x[/latex] is close to 1, the values of [latex]f(x)[/latex] are getting very close to 3. We can get [latex]f(x)[/latex] as close to 3 as we want by taking [latex]x[/latex] very close to 1 so \[\lim\limits_{x\to 1} \dfrac{2x^2-x-1}{x-1}=3.\]

Using algebra: We could have found the same result by noting that \[ f(x)= \dfrac{2x^2-x-1}{x-1} = \dfrac{(2x+1)(x-1)}{(x-1)} = 2x+1\] as long as [latex]x \neq 1[/latex]. (If [latex]x\neq 1[/latex], then [latex]x–1 \neq 0[/latex] so it is valid to divide the numerator and denominator by the factor [latex]x–1[/latex].) The “[latex]x\to 1[/latex]” part of the limit means that x is close to 1 but not equal to 1, so our division step is valid and \[ \lim\limits_{x\to 1}\dfrac{2x^2-x-1}{x-1} = \lim\limits_{x\to 1} 2x+1 = 3,\] which is our answer.
Using a graph: We can graph [latex]y=f(x)= \dfrac{2x^2-x-1}{x-1}[/latex] for [latex]x[/latex] close to 1:
graph
Notice that whenever [latex]x[/latex] is close to 1, the values of [latex]y = f(x)[/latex] are close to 3. Since [latex]f[/latex] is not defined at [latex]x = 1[/latex], the graph has a hole above [latex]x = 1[/latex], but we only care about what [latex]f(x)[/latex] is doing for [latex]x[/latex] close to but not equal to 1.

Example 3

Find [latex]\lim \limits_{x\to 3} \dfrac{\frac{1}{x} -\frac{1}{3} }{x-3}[/latex]

Answer:

Notice that this function is not defined at [latex]x = 3[/latex]. We can find the limit using algebra. Giving the two terms in the numerator a common denominator, we can simplify:

\[ \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \frac{\frac{1}{x} \cdot \frac{3}{3} -\frac{1}{3} \cdot \frac{x}{x} }{x-3} = \frac{\frac{3}{3x} -\frac{x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{x-3} \]
Remember that dividing a fraction is the same as multiplying by the reciprocal, so
\[\frac{\frac{3-x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{\frac{x-3}{1} }\] is equivalent to \[\frac{3-x}{3x} \cdot \frac{1}{x-3}\]
To simplify further, we need to factor a negative 1 out of the numerator. Then we can cancel the term [latex]\left(x-3\right)[/latex]
[latex]\dfrac{-1(x-3)}{3x} \cdot \dfrac{1}{x-3} =\dfrac{-1}{3x}[/latex] as long as [latex]x \neq 3[/latex]
Now we can evaluate the limit using this simplified form.
\[\lim\limits_{x\to 3} \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \lim\limits_{x\to 3} \frac{-1}{3x} = -\frac{1}{9} \]

 

View video of another example.

(by Eric Bancroft, licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License)

One Sided Limits

Sometimes, what happens to us at a place depends on the direction we use to approach that place. If we approach Niagara Falls from the upstream side, then we will be 182 feet higher and have different worries than if we approach from the downstream side. Similarly, the values of a function near a point may depend on the direction we use to approach that point.

Definition (Left and Right Limits)

The left limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches [latex]c[/latex] is [latex]L[/latex] if the values of [latex]f(x)[/latex] get as close to [latex]L[/latex] as we want when [latex]x[/latex] is very close to and left of [latex]c[/latex] (i.e., [latex]x \lt c[/latex]). We write \[\lim\limits_{x\to c^-} f(x)=L.\]
The right limit of [latex]f(x)[/latex] as [latex]x[/latex] approaches [latex]c[/latex] is [latex]L[/latex] if the values of [latex]f(x)[/latex] get as close to [latex]L[/latex] as we want when [latex]x[/latex] is very close to and right of [latex]c[/latex] (i.e., [latex]x \gt c[/latex]). We write \[\lim\limits_{x\to c^+} f(x)=L.\]

 

Example 4

Evaluate the one sided limits of the function [latex]f(x)[/latex] graphed below at [latex]x = 0[/latex] and [latex]x = 1[/latex].
graph
Answer:
As [latex]x[/latex] approach 0 from the left , the value of the function is getting closer to 1, so [latex]\lim\limits_{x\to 0^-} f(x) = 1.[/latex]
As [latex]x[/latex] approaches 0 from the right , the value of the function is getting closer to 2, so [latex]\lim\limits_{x\to 0^+} f(x) = 2.[/latex]
Notice that since the limit from the left and limit from the right are different, the general limit, [latex]\lim\limits_{x\to 0} f(x)[/latex], does not exit.
At [latex]x[/latex] approaches 1 from either direction, the value of the function is approaching 1, so \[\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1} f(x) = 1. \]

See the analysis of limits through a video of another example.

(by Eric Bancroft, licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License)

Continuity

A function that is “friendly” and doesn’t have any breaks or jumps in it is called continuous. More formally,

Definition (Continuity at a Point)

A function [latex]f(x)[/latex] is continuous at [latex]x = a[/latex] if and only if [latex]\lim\limits_{x\to a} f(x) = f(a)[/latex].

 

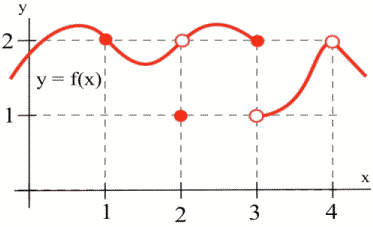
The graph below illustrates some of the different ways a function can behave at and near a point, and the table contains some numerical information about the function and its behavior.
graph
[latex]a[/latex] [latex]f(a)[/latex] [latex]\lim\limits_{x\to a} f(x)[/latex]
1 2 2
2 1 2
3 2 Does not exist (DNE)
4 Undefined 2
Based on the information in the table, we can conclude that [latex]f[/latex] is continuous at 1 since [latex]\lim\limits_{x\to 1} f(x) = 2 = f(1)[/latex]. We can also conclude from the information in the table that [latex]f[/latex] is not continuous at 2 or 3 or 4, because [latex]\lim\limits_{x\to 2} f(x) \neq f(2)[/latex], [latex]\lim\limits_{x\to 3} f(x) \neq f(3)[/latex], and [latex]\lim\limits_{x\to 4} f(x) \neq f(4)[/latex].
The behaviors at [latex]x = 2[/latex] and [latex]x = 4[/latex] exhibit a hole in the graph, sometimes called a removable discontinuity , since the graph could be made continuous by changing the value of a single point. The behavior at [latex]x = 3[/latex] is called a jump discontinuity , since the graph jumps between two values.
So which functions are continuous? It turns out pretty much every function you’ve studied is continuous where it is defined: polynomial, radical, rational, exponential, and logarithmic functions are all continuous where they are defined . Moreover, any combination of continuous functions is also continuous .
This is helpful, because the definition of continuity says that for a continuous function, [latex]\lim\limits_{x\to a} f(x) = f(a)[/latex]. That means for a continuous function, we can find the limit by direct substitution (evaluating the function) if the function is continuous at [latex]a[/latex].

Review video: Continuity

(by Eric Bancroft, licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License)

Example 5

Evaluate using continuity, if possible:

a. [latex]\lim\limits_{x\to 2} x^3-4x[/latex]

b. [latex]\lim\limits_{x\to 2} \dfrac{x-4}{x+3}[/latex]

c. [latex]\lim\limits_{x\to 2} \dfrac{x-4}{x-2}[/latex]

Answer:

a. The given function is polynomial, and is defined for all values of x, so we can find the limit by direct substitution:\[ \lim\limits_{x\to 2} x^3-4x = 2^3-4(2) = 0. \]

b. The given function is rational. It is not defined at x = -3, but we are taking the limit as x approaches 2, and the function is defined at that point, so we can use direct substitution:\[ \lim\limits_{x\to 2} \dfrac{x-4}{x+3} = \dfrac{2-4}{2+3}= -\dfrac{2}{5}. \]
c. This function is not defined at x = 2, and so is not continuous at x = 2. We cannot use direct substitution.

 

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Mathematical Analysis for Business Copyright © 2021 by Ana Duff is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book