"

12.1 Linear Equations

LEARNING OBJECTIVES

  • Identify a linear equation, graphically or algebraically.

In this chapter, we will be studying simple linear regression, which models the linear relationship between two variables [latex]x[/latex] and [latex]y[/latex]. A linear equation has the form [latex]y=b_0+b_1x[/latex] where [latex]b_0[/latex] is the [latex]y[/latex]-intercept of the line and [latex]b_1[/latex] is the slope of the line. For example, [latex]y=3+2x[/latex] and [latex]y=1-4x[/latex] are examples of linear equations. The graph of linear equation is a straight line.

EXAMPLE

The equation [latex]y=-1+2x[/latex] is a linear equation. The slope is [latex]2[/latex] and the [latex]y[/latex]-intercept is [latex]-1[/latex]. The graph of [latex]y=-1+2x[/latex] is shown below.

Graph of the equation y = -1 + 2x. This is a straight line that crosses the y-axis at -1 and is sloped up and to the right, rising 2 units for every one unit of run.

TRY IT

Is the graph shown below the graph of a linear equation?  Why or why not?

This is a graph of an equation. The x-axis is labeled in intervals of 2 from 0 - 14; the y-axis is labeled in intervals of 2 from 0 - 12. The equation's graph is a curve that crosses the y-axis at 2 and curves upward and to the right.

Click to see Solution

 

This is not a linear equation because the graph is not a straight line.

The slope [latex]b_1[/latex] is a number that describes the steepness of a line. The slope tells us how the value of the [latex]y[/latex] variable will change for every one-unit increase in the value of the [latex]x[/latex] variable.

The [latex]y[/latex]-intercept [latex]b_0[/latex] is the value of the [latex]y[/latex]-coordinate where the graph of the line crosses the [latex]y[/latex]-axis. Algebraically, the [latex]y[/latex]-intercept is the value of [latex]y[/latex] when [latex]x=0[/latex].

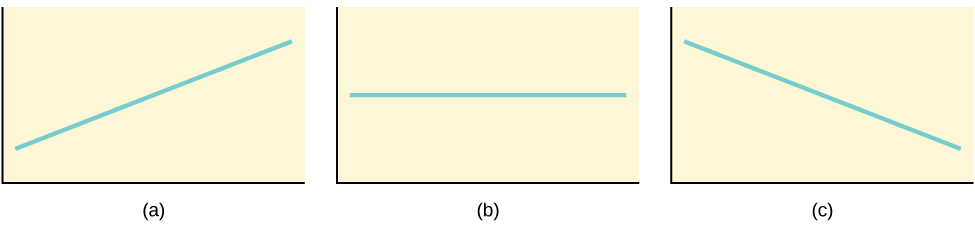
Consider the figure below, which illustrates three different linear equations:

  • In (a), the line rises from left to right across the graph. This means that the slope [latex]b_1[/latex] is a positive number ([latex]b_1 \gt 0[/latex]).
  • In (b), the line is horizontal (parallel to the [latex]x[/latex]-axis). This means that the slope [latex]b_1[/latex] is zero ([latex]b_1=0[/latex]).
  • In (c), the line falls from left to right across the graph. This means that the slope [latex]b_1[/latex] is a negative number ([latex]b_1 \lt 0[/latex]).

 

Three possible graphs of the equation y = a + bx. For the first graph, (a), b > 0 and so the line slopes upward to the right. For the second, b = 0 and the graph of the equation is a horizontal line. In the third graph, (c), b < 0 and the line slopes downward to the right.

EXAMPLE

Consider the linear equation [latex]y=-25+15x[/latex].

  • The slope is [latex]15[/latex].  This tells us that when the value of [latex]x[/latex] increases by [latex]1[/latex], the value of [latex]y[/latex] increases by [latex]15[/latex]. Because the slope is positive, the graph of [latex]y=-25+15x[/latex] rises from left to right.
  • The [latex]y[/latex]-intercept is [latex]-25[/latex]. This tells us that when [latex]x=0[/latex], [latex]y=-25[/latex].  On the graph of [latex]y=-25+15x[/latex], the line crosses the [latex]y[/latex]-axis at [latex]-25[/latex].

TRY IT

Consider the linear equation [latex]y=17-10x[/latex]. Identify the slope and [latex]y[/latex]-intercept. Describe the slope and [latex]y[/latex]-intercept in sentences.

 

Click to see Solution
  • The slope is [latex]-10[/latex]. This tells us that when the value of [latex]x[/latex] increases by [latex]1[/latex], the value of [latex]y[/latex] decreases by [latex]10[/latex]. Because the slope is negative, the graph of [latex]y=17-10x[/latex] falls from left to right.
  • The [latex]y[/latex]-intercept is [latex]17[/latex]. This tells us that when [latex]x=0[/latex], [latex]y=17[/latex]. On the graph of [latex]y=17-10x[/latex], the line crosses the [latex]y[/latex]-axis at [latex]17[/latex].

Exercises

  1. Is the equation [latex]y=10+5x–3x^2[/latex] linear? Why or why not?
    Click to see Answer

    Not linear.

     

  2. Which of the following equations are linear?
    1. [latex]y=6x+8[/latex]
    2. [latex]y+7=3x[/latex]
    3. [latex]y–x=8x^2[/latex]
    4. [latex]4y=8[/latex]
    Click to see Answer

    (a), (b), and (d) are linear.

     

  3. The price of a single issue of stock can fluctuate throughout the day. A linear equation that represents the price of stock for Shipment Express is [latex]y=15–1.5x[/latex] where [latex]x[/latex] is the number of hours passed in an eight-hour day of trading.
    1. What is the slope? Interpret the slope’s meaning in the context of the question.
    2. What is the [latex]y[/latex]-intercept? Interpret the [latex]y[/latex]-intercept’s meaning in the context of the question.
    3. If you owned this stock, would you want a positive or negative slope? Why?
    Click to see Answer
    1. [latex]-1.5[/latex]. For each additional hour that passes during the trading day, the price of the stock decreases by [latex]\$1.50[/latex].
    2. [latex]15[/latex]. At the start of the trading day, the price of the stock is [latex]\$15[/latex].
    3. Positive slope because that means the price of the stock is increasing.

     

“12.2 Linear Equations” and “12.8 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics - Second Edition Copyright © 2025 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book