"

10.1 The Chi Square Distribution

LEARNING OBJECTIVES

  • Find the area under a [latex]\chi^2[/latex]-distribution.
  • Find the [latex]\chi^2[/latex]-score for a given area under the curve of a [latex]\chi^2[/latex]-distribution.

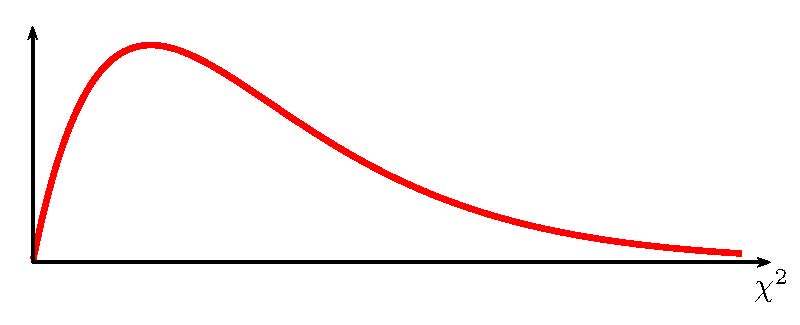
The [latex]\chi^2[/latex]-distribution is a continuous probability distribution. The graph of a [latex]\chi^2[/latex]-distribution is shown below.

The image shows a chi-square distribution curve. It is asymmetrical and slopes downward continually.

 

Properties of the [latex]\chi^2[/latex]-distribution:

  • The graph of a [latex]\chi^2[/latex]-distribution is positively skewed and asymmetrical with a minimum value of 0 and no maximum value.
  • A [latex]\chi^2[/latex]-distribution is determined by its degrees of freedom, [latex]df[/latex].  The value of the degrees of freedom depends on how the [latex]\chi^2[/latex]-distribution is used.  There is a different [latex]\chi^2[/latex]-distribution for every value of [latex]df[/latex].  As the degrees of freedom increase, the [latex]\chi^2[/latex]-distribution approaches a normal distribution.
  • The total area under the graph of a [latex]\chi^2[/latex]-distribution is 1.
  • The mean of a [latex]\chi^2[/latex]-distribution is its degrees of freedom:  [latex]\mu=df[/latex].
  • The variance of a [latex]\chi^2[/latex]-distribution is twice its degrees of freedom:  [latex]\sigma^2=2\times df[/latex].
  • The mode of a [latex]\chi^2[/latex]-distribution is [latex]df-2[/latex].  The peak of the graph occurs at the mode.
  • Probabilities associated with a [latex]\chi^2[/latex]-distribution are given by the area under the curve of the [latex]\chi^2[/latex]-distribution.

USING EXCEL TO CALCULATE THE AREA UNDER A [latex]{\color{white}{\chi^2}}[/latex]-DISTRIBUTION

To find the area in the left tail:

  • To find the area under a [latex]\chi^2[/latex]-distribution to the left of a given [latex]\chi^2[/latex]-score, use the chisq.dist([latex]\chi^2[/latex], degrees of freedom, logic operator) function.
    • For [latex]\chi^2[/latex], enter the [latex]\chi^2[/latex]-score.
    • For degrees of freedom, enter the value of the degrees of freedom for the [latex]\chi^2[/latex]-distribution.
    • For logic operator, enter true.
  • The output from the chisq.dist function is the area to the left of the entered [latex]\chi^2[/latex]-score.
  • Visit the Microsoft page for more information about the chisq.dist function.

To find the area in the right tail:

  • To find the area under a [latex]\chi^2[/latex]-distribution to the right of a given [latex]\chi^2[/latex]-score, use the chisq.dist.rt([latex]\chi^2[/latex], degrees of freedom) function.
    • For [latex]\chi^2[/latex], enter the [latex]\chi^2[/latex]-score.
    • For degrees of freedom, enter the value of the degrees of freedom for the [latex]\chi^2[/latex]-distribution.
  • The output from the chisq.dist.rt function is the area to the right of the entered [latex]\chi^2[/latex]-score.
  • Visit the Microsoft page for more information about the chisq.dist.rt function.

EXAMPLE

Consider a [latex]\chi^2[/latex]-distribution with [latex]12[/latex] degrees of freedom.

  1. Find the area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2=3.71[/latex].
  2. Find the area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2=6.29[/latex].

Solution

  1. Function chisq.dist
    Field 1 3.71
    Field 2 12
    Field 3 true
    Answer 0.0119
  2. Function chisq.dist.rt
    Field 1 6.72
    Field 2 12
    Answer 0.8755

USING EXCEL TO CALCULATE [latex]{\color{white}{\chi^2}}[/latex]-SCORES

To find the [latex]\chi^2[/latex]-score for a given left-tail area:

  • To find the [latex]\chi^2[/latex]-score for a given area under the [latex]\chi^2[/latex]-distribution to the left of the [latex]\chi^2[/latex]-score, use the chisq.inv(area to the left, degrees of freedom) function.
    • For area to the left, enter the area to the left of required [latex]\chi^2[/latex]-score.
    • For degrees of freedom, enter the value of the degrees of freedom for the [latex]\chi^2[/latex]-distribution.
  • The output from the chisq.inv function is the value of the [latex]\chi^2[/latex]-score so that the area to the left of the [latex]\chi^2[/latex]-score is the entered area.
  • Visit the Microsoft page for more information about the chisq.inv function.

To find the [latex]\chi^2[/latex]-score for a given right-tail area:

  • To find the [latex]\chi^2[/latex]-score for a given area under the [latex]\chi^2[/latex]-distribution to the right of the [latex]\chi^2[/latex]-score, use the chisq.inv.rt(area to the right, degrees of freedom) function.
    • For area to the right, enter the area to the right of required [latex]\chi^2[/latex]-score.
    • For degrees of freedom, enter the value of the degrees of freedom for the [latex]\chi^2[/latex]-distribution.
  • The output from the chisq.inv.rt function is the value of the [latex]\chi^2[/latex]-score so that the area to the right of the [latex]\chi^2[/latex]-score is the entered area.
  • Visit the Microsoft page for more information about the chisq.inv.rt function.

EXAMPLE

Consider a [latex]\chi^2[/latex]-distribution with [latex]37[/latex] degrees of freedom.

  1. Find the [latex]\chi^2[/latex]-score so that the area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2[/latex] is [latex]0.25[/latex].
  2. Find the [latex]\chi^2[/latex]-score so that the area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2[/latex] is [latex]0.148[/latex].

Solution

  1. Function chisq.inv
    Field 1 0.25
    Field 2 37
    Answer 30.89
  2. Function chisq.dist.rt
    Field 1 0.148
    Field 2 37
    Answer 45.97

TRY IT

Consider a [latex]\chi^2[/latex]-distribution with [latex]28[/latex] degrees of freedom.

  1. Find the area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2=21.7[/latex].
  2. Find the [latex]\chi^2[/latex]-score so that area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2[/latex] is [latex]0.3[/latex].
  3. Find the [latex]\chi^2[/latex]-score so that area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2[/latex] is [latex]0.42[/latex].
  4. Find the area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2=17.3[/latex].
Click to see Solution
  1. Function chisq.dist.rt
    Field 1 21.7
    Field 2 28
    Answer 0.795
  2. Function chisq.inv
    Field 1 0.3
    Field 2 28
    Answer 23.65
  3. Function chisq.inv.rt
    Field 1 0.42
    Field 2 28
    Answer 28.85
  4. Function chisq.dist
    Field 1 17.3
    Field 2 28
    Field 3 true
    Answer 0.0576

Exercises

  1. If the number of degrees of freedom for a [latex]\chi^2[/latex]-distribution is [latex]25[/latex], what is the population mean and standard deviation?
    Click to see Answer

    [latex]\text{mean}=25[/latex], [latex]\text{standard deviation}=7.07[/latex]

     

  2. Where is mode located on a [latex]\chi^2[/latex]-distribution curve?
    Click to see Answer

    At the peak of the curve.

     

  3. The variance of a [latex]\chi^2[/latex]-distribution is [latex]36[/latex]. What is the mode?
    Click to see Answer

    [latex]16[/latex]

     

  4. Consider a [latex]\chi^2[/latex]-distribution with [latex]17[/latex] degrees of freedom.
    1. Find the area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2=15.3[/latex].
    2. Find the area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2=22.8[/latex].
    3. Find the [latex]\chi^2[/latex]-score so that area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2[/latex] is [latex]0.291[/latex].
    4. Find the [latex]\chi^2[/latex]-score so that area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2[/latex] is [latex]0.3156[/latex].
    Click to see Answer
    1. [latex]0.426[/latex]
    2. [latex]0.1559[/latex]
    3. [latex]13.4[/latex]
    4. [latex]19.23[/latex]

     

  5. Consider a [latex]\chi^2[/latex]-distribution with [latex]12[/latex] degrees of freedom.
    1. What is the mean of the [latex]\chi^2[/latex]-distribution?
    2. What is the mode of the [latex]\chi^2[/latex]-distribution?
    3. What is the variance of the [latex]\chi^2[/latex]-distribution?
    4. Find the area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2=82[/latex].
    5. Find the area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2=14.9[/latex].
    6. Find the [latex]\chi^2[/latex]-score so that area under the [latex]\chi^2[/latex]-distribution to the left of [latex]\chi^2[/latex] is [latex]0.1183[/latex].
    7. Find the [latex]\chi^2[/latex]-score so that area under the [latex]\chi^2[/latex]-distribution to the right of [latex]\chi^2[/latex] is [latex]0.6977[/latex].
    Click to see Answer
    1. [latex]12[/latex]
    2. [latex]10[/latex]
    3. [latex]24[/latex]
    4. [latex]0.2307[/latex]
    5. [latex]0.2470[/latex]
    6. [latex]6.62[/latex]
    7. [latex]9.06[/latex]

     

“10.2 The Chi Square Distribution” and “10.6 Exercises” from Introduction to Statistics by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Statistics - Second Edition Copyright © 2025 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book