9.2.3 Plans d’expériences : plans fractionnaires
9.2.7 Plans fractionnaires
Avec 2k essais, il est évident qu’en augmentant le nombre de facteurs (k), la quantité de ressources nécessaires augmentera rapidement. Il est donc nécessaire de discuter des méthodes permettant de réduire la quantité de travail à effectuer et d’économiser des ressources. Cela s’applique surtout aux scénarios de sélection ou d’évaluation d’un nouveau système, comme une exploration à l’échelle du laboratoire, la fabrication d’un nouveau produit ou même la résolution d’un problème.
Ce concept repose sur l’utilisation de la notion de confusion, introduite précédemment à la section 9.2.6. En confondant les facteurs les uns avec les autres, on peut réduire le nombre d’essais nécessaires, ce qui permet de diviser par deux la quantité de travail requise. Une expérience de 2k essais peut devenir une expérience de 2k-1 essais grâce à ce principe. C’est ce qu’on appelle un plan fractionné. Ce principe fonctionne parce qu’on s’intéresse généralement davantage aux effets principaux et parce que les interactions n’ont qu’une signification pratique limitée (surtout lorsqu’il y a trois facteurs ou plus).
Exemple 9.2.7.1 Plans fractionnaires
Comme le montre le tableau 9.2.7.1, on peut prendre une expérience de 23 (huit) essais et la réduire de moitié à quatre essais en confondant un facteur avec l’interaction des deux autres facteurs. On écrit les deux premiers facteurs comme des facteurs normaux, mais le troisième facteur prend la forme du produit des deux premiers facteurs.
| Essai | A | B | C = AB |
| 1 | – | – | + |
| 2 | + | – | – |
| 3 | – | + | – |
| 4 | + | + | + |
Maintenant, il est important de se demander quelles sont les conséquences de cette approche.
1) Ça réduit le travail de moitié! On ne saurait trop insister sur ce point. On a réduit la quantité de ressources utilisées et amélioré l’efficacité du processus, surtout si on considère que les premières expériences ne permettront pas de trouver les paramètres optimaux et qu’il faudra mener plusieurs expériences pour les déterminer (voir la section 9.3).
2) Il y a maintenant plusieurs facteurs confondus. Chacun des effets principaux (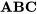 ) est désormais confondu avec un terme d’interaction.
) est désormais confondu avec un terme d’interaction.
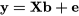
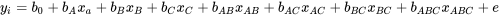
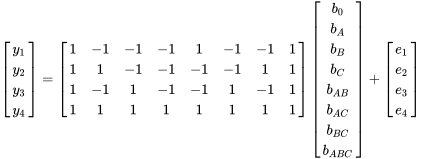
Il devrait être évident que ce système est maintenant sous-déterminé puisqu’il y a huit inconnues, mais seulement quatre équations (comme il n’y a eu que quatre essais). En outre, la matrice X n’est plus orthogonale. Pour y remédier, il faut faire exactement ce qui a été dit plus haut, à savoir confondre les effets principaux avec les termes d’interaction. Ceci est illustré ci-dessous :

Par exemple, on dirait maintenant que l’effet principal de 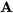 est confondu avec l’interaction de
est confondu avec l’interaction de 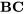 , puisque le coefficient du modèle est la somme de ces deux effets. On peut donc affirmer que
, puisque le coefficient du modèle est la somme de ces deux effets. On peut donc affirmer que 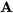 est un alias de
est un alias de 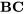 , que
, que 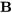 est un alias de
est un alias de 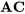 , que
, que 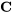 est un alias de
est un alias de 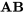 et que l’ordonnée à l’origine est un alias de l’interaction à trois facteurs
et que l’ordonnée à l’origine est un alias de l’interaction à trois facteurs 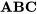 . Ceci peut être exprimé par les équations ci-dessous.
. Ceci peut être exprimé par les équations ci-dessous.
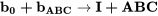
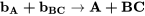
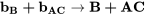
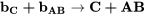
10.8 Générateurs
Pour un système à trois facteurs, il est assez simple de déterminer comment confondre les facteurs. Toutefois, lorsqu’il y a plus de facteurs, c’est beaucoup plus compliqué. Pour simplifier ce processus, on peut utiliser des générateurs.
Pour un système à quatre facteurs (24), il y aurait les facteurs 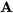 ,
, 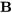 ,
, 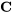 et
et 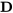 . Les facteurs
. Les facteurs 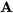 à
à 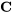 seraient considérés comme normaux, mais le facteur
seraient considérés comme normaux, mais le facteur 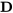 s’écrirait
s’écrirait 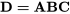 . C’est ce qu’on appelle la relation génératrice.
. C’est ce qu’on appelle la relation génératrice.
Pour travailler avec une relation génératrice, il faut connaître certaines règles :
- L’ordonnée à l’origine
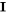 est une colonne de uns.
est une colonne de uns. - La multiplication d’un facteur par lui-même donne l’identité (ou l’ordonnée à l’origine) :
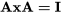
- Un facteur multiplié par l’identité (ou l’ordonnée à l’origine [une colonne de uns]) est égal à lui-même :
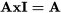
- Grâce à un peu d’algèbre, on peut également établir la relation de définition
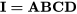 . Prenons la relation génératrice et multiplions les deux côtés par
. Prenons la relation génératrice et multiplions les deux côtés par 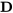 . On obtient alors [latex]\mathbf{D} \times \mathbf{D} = \mathbf{ABC} \times \mathbf{D][/latex]. Or, [latex]\mathbf{D} \times \mathbf{D} = \mathbf{I}[/latex], d’où [latex]\mathbf{I = {ABCD}}[/latex].
. On obtient alors [latex]\mathbf{D} \times \mathbf{D} = \mathbf{ABC} \times \mathbf{D][/latex]. Or, [latex]\mathbf{D} \times \mathbf{D} = \mathbf{I}[/latex], d’où [latex]\mathbf{I = {ABCD}}[/latex].
En multipliant un effet principal par la relation de définition, on peut rapidement déterminer le facteur avec lequel il est aliasé (ou confondu). Par exemple, pour la moitié 24-1, on peut voir que 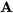 est aliasé avec
est aliasé avec 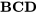 par l’équation suivante :
par l’équation suivante :

On sait que pour la moitié 23-1 , la relation génératrice est 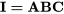 , ce qui indique que
, ce qui indique que 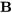 est aliasé avec
est aliasé avec 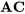 , puisque
, puisque 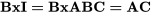
9.2.9 Résolution
La confusion et l’utilisation de plans fractionnés entraînent un compromis en ce qui concerne la résolution, la mesure dans laquelle un ou des effets principaux estimés sont aliasés avec des interactions estimées à deux niveaux, trois niveaux ou plus. La résolution correspond à l’ordre de la plus petite interaction confondue avec un effet principal, plus un. Le tableau de compromis ci-dessous (figure 9.2.9.1) permet de visualiser ce phénomène.
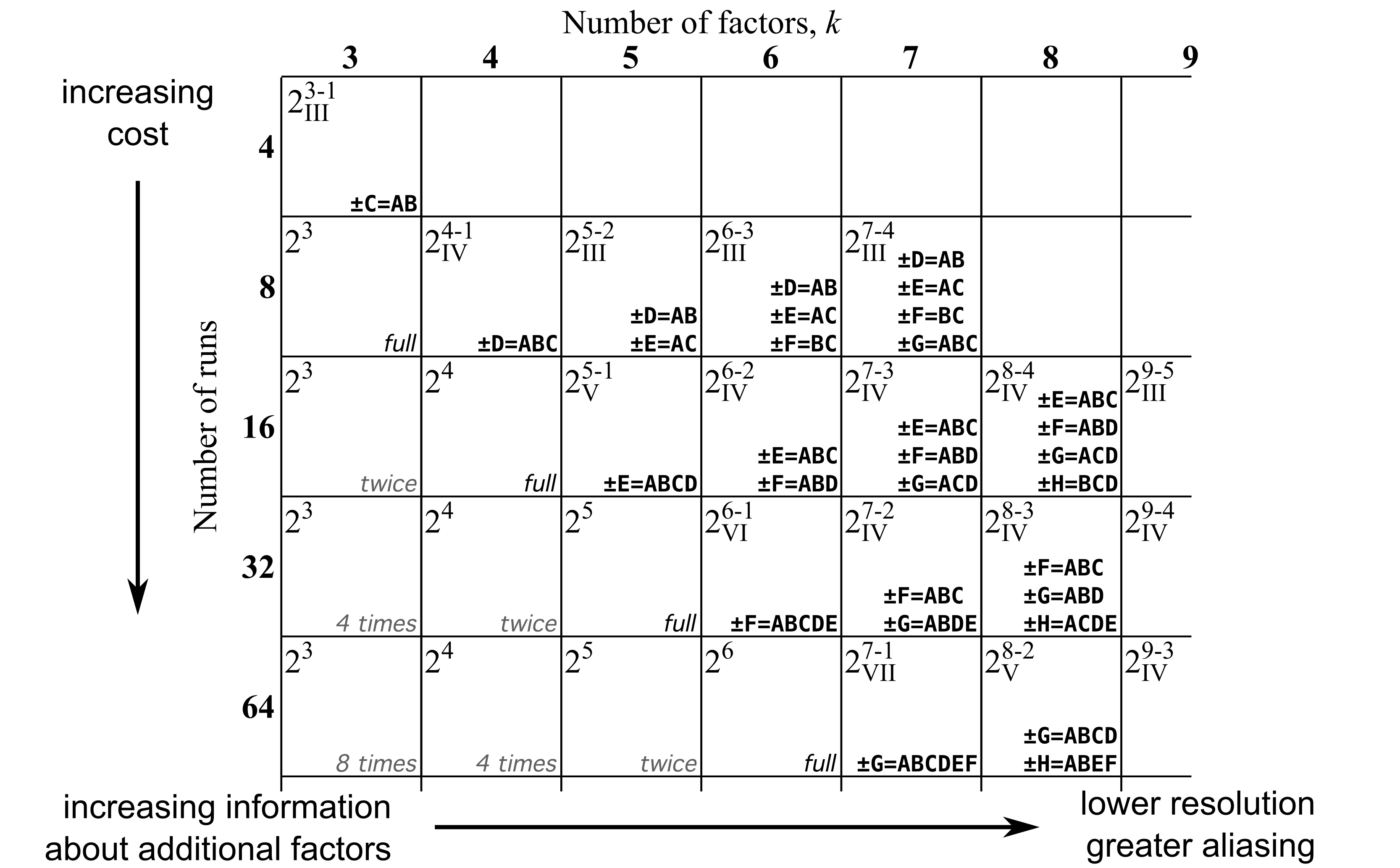
Prenons l’exemple de : 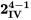 . Ici, les chiffres romains
. Ici, les chiffres romains 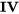 indiquent le niveau de résolution du plan. Ce nombre est équivalent au nombre de facteurs présents dans la relation de définition. Puisque
indiquent le niveau de résolution du plan. Ce nombre est équivalent au nombre de facteurs présents dans la relation de définition. Puisque 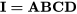 pour une expérience
pour une expérience 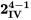 on dit qu’il s’agit d’un plan de résolution
on dit qu’il s’agit d’un plan de résolution 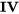 .
.
De manière générale :
- les plans de résolution III sont bons pour le tri
- les plans de résolution IV sont bons pour la caractérisation
- les plans de résolution V sont bons pour l’optimisation
Il convient de noter qu’aucun de ces plans ne comporte de confusion entre les effets principaux.
Caractéristiques uniques des plans de résolution III, IV et V
Plans de résolution III :
- Effets principaux confondus avec des interactions à deux facteurs
Plans de résolution IV :
- Effets principaux confondus avec des interactions à trois facteurs.
- Interactions à deux facteurs confondues entre elles.
Plans de résolution V :
- Pas d’aliassage entre les effets principaux et les interactions à deux facteurs.
- Interactions à deux facteurs sont aliasées avec des interactions à trois facteurs.
