9.2.2 Plans d’expériences : perturbations et blocage
9.2.5 Comprendre les perturbations
Toute expérience comporte des éléments externes qui peuvent avoir ou auront une influence sur les résultats. Ces éléments se nomment des perturbations. En tant que scientifiques ou ingénieur.e.s, il nous appartient de concevoir des expériences qui réduisent autant que possible l’impact des perturbations.
D’une manière générale, on peut classer les perturbations comme suit :
- connues ou inconnues
- contrôlables ou incontrôlables
- mesurables ou non mesurables
Dans un monde idéal, toutes les perturbations seraient connues, contrôlables et mesurables, mais ce n’est presque jamais le cas. La température ambiante, un changement inattendu sur le marché boursier, le choix d’un.e machiniste, etc. sont des facteurs qui ne peuvent pas être contrôlés ou même planifiés, et c’est la raison pour laquelle la randomisation est si importante. La randomisation permet d’éviter que des perturbations n’affectent systématiquement le résultat.
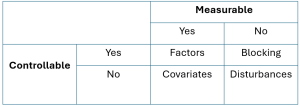
Une méthode courante pour gérer les perturbations consiste à concevoir l’expérience de manière à en tenir compte. Si la perturbation est contrôlée et maintenue constante pour toutes les expériences, il ne s’agit plus d’une perturbation puisque son effet s’annule. L’appariement peut également annuler l’effet des perturbations en utilisant le même sujet/les mêmes échantillons pour les raisons indiquées à la partie 5. On peut classer les facteurs en fonction de leur capacité à être contrôlés ou mesurés (tableau 9.2.5.1). Les covariables sont des paramètres susceptibles de modifier le résultat, mais qui ne nous intéressent pas. La température ambiante en est un exemple. Pour de nombreuses expériences, la température ne présente pas d’intérêt majeur, mais elle pourrait influencer le résultat. Le blocage sera abordé à la section 9.2.6.
9.2.6 Blocage (et confusion)
Grâce à un plan astucieux, le blocage nous permet de minimiser l’impact d’une perturbation sur l’interprétation du système. Le blocage est utilisé lorsqu’on sait qu’il y a des perturbations, mais qu’on ne peut pas les contrôler. La solution est de confondre délibérément l’effet de la perturbation avec un autre effet du système qui devrait être faible (ou insignifiant).
Prenons l’exemple d’un système à trois facteurs, A, B et C. Dans les plans factoriels, les termes d’interaction d’ordre supérieur ont généralement une incidence très faible sur le résultat, ce qui en fait des coefficients intéressants à confondre avec une perturbation. De fait, il sera impossible de faire la différence entre l’effet d’interaction de ABC et la perturbation. On pourrait aussi dire que le coefficient correspondant est : 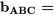 = effet d’interaction de ABC + perturbation.
= effet d’interaction de ABC + perturbation.
Ce concept peut être combiné avec des essais expérimentaux pour utiliser un processus appelé blocage. Normalement, avec trois facteurs, il y aurait 23 expériences. Mais avec le blocage, on divise les essais en deux, de sorte que la moitié des essais s’effectue à ABC+, et l’autre moitié, à ABC-.
Exemple 9.2.6.1 Blocage (et confusion)
Prenons l’exemple d’une expérience de marketing pour une application mobile, dont le résultat mesuré est le nombre d’achats dans l’application 60 jours après le marketing. Les trois facteurs sont la promotion (A), le message envoyé (B) et le prix (C). Cependant, on constate rapidement que certaines personnes de l’étude auront des iPhone, tandis que d’autres auront des téléphones Android. Le type de téléphone des utilisateurs correspond aux critères d’un facteur mesurable, mais non contrôlable. Le tableau 9.2.6.1 montre comment cela se conceptualise.
| Expérience | A (Promotion) | B (Message) | C (Prix) | AB | AC | BC | ABC (Confondu) |
| 1 | – | – | – | + | + | + | – (iPhone) |
| 2 | + | – | – | – | – | + | + (Android) |
| 3 | – | + | – | – | + | – | + (Android) |
| 4 | + | + | – | + | – | – | – (iPhone) |
| 5 | – | – | + | + | – | – | + (Android) |
| 6 | + | – | + | – | + | – | – (iPhone) |
| 7 | – | + | + | – | – | + | – (iPhone) |
| 8 | + | + | + | + | + | + | + (Android) |
Il y a inévitablement une certaine confusion, car l’effet du terme d’interaction ABC et du type de téléphone ne peut être séparé. Cependant, ce compromis est bénéfique, car les effets principaux et les interactions à deux facteurs peuvent être interprétés sans biais en supposant que la perturbation a été maintenue constante.
