9.2.1 Plans d’expériences : plans factoriels complets
9.2.1 Plans factoriels complets
Comme illustré aux sections 9.1.3 et 9.1.5, on peut utiliser un plan d’expériences pour étudier les effets de plusieurs facteurs simultanément. Cette approche est plus efficace pour recueillir des informations sur un système.
En fin de compte, il faut déterminer le nombre d’expériences nécessaires. Selon le nombre de facteurs (k) et le nombre correspondant de niveaux (X), le nombre d’expériences dans un plan factoriel est donné par : Xk.
Dans l’exemple des biscuits de la section 9.1.3, il y avait deux facteurs (luminosité et prix), et chaque facteur avait deux niveaux. Par conséquent, il y avait 22 expériences, soit 4 expériences dans ce plan factoriel. Naturellement, cette méthode peut être étendue à trois, quatre ou cinq facteurs (ou même plus), ce qui donne respectivement 8, 16 et 32 expériences en supposant que chaque facteur a deux niveaux. On parle alors de plans factoriels complets.
9.2.2 Application de la régression linéaire aux plans factoriels
Supposons maintenant que l’on applique un modèle de régression linéaire à un plan factoriel pour lequel on dispose de quatre paramètres à estimer et de quatre points de données. Autrement dit, il n’y aura aucun degré de liberté et, par conséquent, il n’y aura aucune erreur résiduelle. Cela signifie qu’on ne peut pas effectuer de tests d’hypothèse sur les paramètres ni générer d’intervalles de confiance. Dans la section 9.2.3, nous verrons comment ajuster le plan de manière à obtenir des erreurs résiduelles et à pouvoir calculer les tests d’hypothèse souhaités.
Exemple 9.2.2.1 : Application de la régression linéaire aux plans factoriels
Pour l’instant, en utilisant l’exemple de la section 9.1.5 (voir tableau 9.2.2.1), on peut générer le modèle de régression des moindres carrés suivant pour l’échantillon :
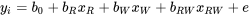
| Expérience | Essai | Rugosité de la surface | Angle de contact avec l’eau | Viabilité cellulaire en unités arbitraires (u.a.) |
| 1 | 4 | −(300 µm) | −(50°) | 31 |
| 2 | 1 | +(350 µm) | −(50°) | 70 |
| 3 | 2 | −(300 µm) | +(100°) | 56 |
| 4 | 3 | +(350 µm) | +(100°) | 82 |
Pour conceptualiser cet ensemble d’expériences, on peut utiliser les matrices ci-dessous (où 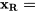 = la rugosité de surface et
= la rugosité de surface et 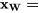 = l’angle de contact avec l’eau) :
= l’angle de contact avec l’eau) :
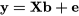
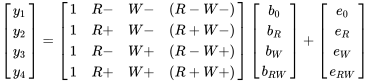
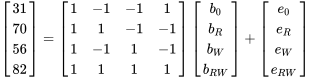
On peut résoudre ce système à l’aide de nos connaissances en régression linéaire. Comme le système est orthogonal, la matrice 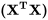 n’a que des valeurs non nulles sur la diagonale. Par conséquent :
n’a que des valeurs non nulles sur la diagonale. Par conséquent :
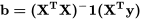
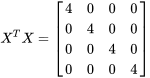


L’équation résultante, 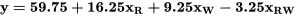 , peut être interprétée de la même manière que précédemment. Par exemple, une augmentation d’une unité de la rugosité correspond à une augmentation de 16,25 u.a. de la viabilité cellulaire. Cette méthode explique également pourquoi il avait fallu diviser par 2 une deuxième fois précédemment, puisque ce coefficient représente l’effet du passage de la rugosité de surface de 0 à 1, soit de 325 à 350 µm. Il en va de même pour l’angle de contact avec l’eau. Enfin, le terme d’interaction diminue la viabilité cellulaire de 3,25 unités si la rugosité de la surface et l’angle de contact avec l’eau sont au même niveau (tous deux élevés ou tous deux faibles).
, peut être interprétée de la même manière que précédemment. Par exemple, une augmentation d’une unité de la rugosité correspond à une augmentation de 16,25 u.a. de la viabilité cellulaire. Cette méthode explique également pourquoi il avait fallu diviser par 2 une deuxième fois précédemment, puisque ce coefficient représente l’effet du passage de la rugosité de surface de 0 à 1, soit de 325 à 350 µm. Il en va de même pour l’angle de contact avec l’eau. Enfin, le terme d’interaction diminue la viabilité cellulaire de 3,25 unités si la rugosité de la surface et l’angle de contact avec l’eau sont au même niveau (tous deux élevés ou tous deux faibles).
9.2.3 Détermination de la signification statistique
Comme mentionné dans la section précédente, en l’absence de degrés de liberté, aucun test d’hypothèse ou intervalle de confiance ne peut être généré pour les effets principaux ou les termes d’interaction.
Dans le cas d’un plan factoriel complet, il y a plusieurs choix :
- Effectuer une série complète de répétitions.
- Ajouter des points centraux.
- Supprimer les facteurs de faible ampleur ou sans intérêt.
- Utiliser un motif de confusion ou un plan fractionnaire.
1) Effectuer une série complète de répétitions
Avec des ressources et un temps infinis, ce serait la méthode la plus simple, car on aurait alors plus d’expériences que de paramètres. Cela permettrait d’obtenir les degrés de liberté nécessaires pour calculer l’erreur-type de tous les coefficients du modèle. Toutefois, il s’agit généralement d’une solution inefficace qui monopolise beaucoup de ressources. Il existe de meilleurs choix, mais c’est toujours une option. Une fois que l’on dispose de degrés de liberté, il est possible de déterminer quels coefficients sont peu significatifs et de les supprimer pour obtenir des degrés de liberté supplémentaires.
2) Ajouter des points centraux
Les points centraux sont des paramètres à mi-chemin entre les niveaux d’un facteur donné. En utilisant l’exemple des biomatériaux, on pourrait mener un essai au point central correspondant à 325 µm de rugosité de surface et à 75° d’angle de contact avec l’eau. Cette opération peut être effectuée autant de fois que souhaité, car l’ajout de ces éléments ne modifie pas l’orthogonalité de X et ajoute des degrés de liberté pour faciliter le calcul de l’erreur standard. L’ajout de points centraux est toujours une option viable, car il ne nécessite pas autant d’essais qu’un ensemble de répétitions. Comme dans le cas d’une répétition complète, une fois qu’on a des degrés de liberté, on peut identifier les coefficients qui sont significatifs ou non, puis en supprimer pour obtenir des degrés de liberté supplémentaires. En notation matricielle, on obtiendrait ceci en effectuant trois répétitions :
Exemple 9.2.2.2 Ajout de répétitions pour obtenir des degrés de liberté
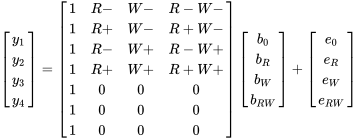
3) Supprimer les facteurs de faible ampleur ou sans intérêt
Avec un plan factoriel complet, on peut également choisir de supprimer un coefficient, même si on ne dispose pas d’intervalles de confiance pour étayer ce choix. Si le coefficient est de l’ordre de 0,00001 mais qu’on travaille dans un contexte pratique où les changements dans le système ont des valeurs de l’ordre de 100 ou 1000, il n’est peut-être pas pratique de conserver le coefficient (même s’il est statistiquement significatif), étant donné qu’il n’a que peu d’intérêt pratique ou clinique. La suppression des coefficients de cette manière doit être effectuée avec prudence : il faut connaître le système et tenir compte du contexte pour éviter de commettre une erreur. Comme dans les deux exemples précédents, on obtiendra des degrés de liberté pour calculer l’erreur standard.
Les diagrammes de Pareto (voir figure 9.2.3.1) sont un moyen de visualiser ce concept. En classant les coefficients par ordre décroissant d’importance (à l’exclusion de l’ordonnée à l’origine) et en les représentant sous la forme d’un diagramme à barres, il est possible de déterminer rapidement les coefficients qui ont le plus de répercussions sur le système.
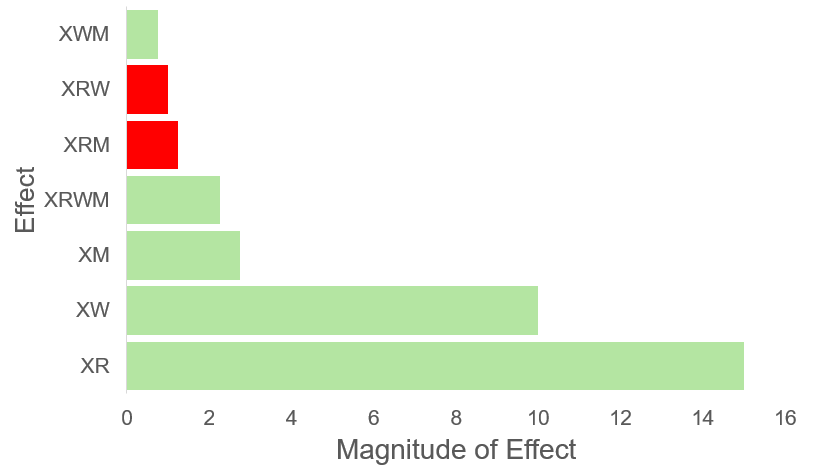
La figure 9.2.3.1 permet de repérer rapidement les coefficients qui ont le plus de répercussions sur les résultats. L’utilisation de couleurs peut également nous permettre de déterminer rapidement quels coefficients ont un effet positif (vert) et lesquels ont un effet négatif (rouge).
4) Utiliser un motif de confusion ou un plan fractionnaire
Voir les sections 9.2.6 et 9.2.7, car il s’agit d’un concept essentiel pour les plans fractionnaires.
9.2.4 Augmenter le nombre de facteurs
Tous les exemples utilisés jusqu’à présent concernaient des situations à deux facteurs. L’augmentation du nombre de facteurs ajoute à la complexité, mais les méthodes et les mathématiques sous-jacentes restent les mêmes.
Exemple 9.2.4.1 : Augmenter le nombre de facteurs
Reprenons l’exemple des biomatériaux et considérons maintenant un troisième facteur, le matériau, car les implants dentaires de l’entreprise ont été conçus pour utiliser soit du titane, soit de l’acier inoxydable. Les tableaux des niveaux (tableau 9.2.4.1), de l’ordre standard (tableau 9.2.4.2) et des résultats expérimentaux (tableau 9.2.4.3) sont présentés ci-dessous.
| Facteur | Niveau faible | Niveau élevé |
| Rugosité de la surface | 300 µm | 350 µm |
| Angle de contact avec l’eau | 50° | 100° |
| Matériau | Titane | Acier inoxydable |
| Expérience | Rugosité de la surface | Angle de contact avec l’eau | Matériau |
| 1 | -1 | -1 | -1 |
| 2 | 1 | -1 | -1 |
| 3 | -1 | 1 | -1 |
| 4 | 1 | 1 | -1 |
| 5 | -1 | -1 | 1 |
| 6 | 1 | -1 | 1 |
| 7 | -1 | 1 | 1 |
| 8 | 1 | 1 | 1 |
| Expérience | Essai | Rugosité de la surface | Angle de contact avec l’eau | Matériau | Viabilité cellulaire en unités arbitraires (u.a.) |
| 1 | 8 | -1 (300 µm) | -1 (50°) | -1 (Titane) | 31 |
| 2 | 5 | +1 (350 µm) | -1 (50°) | -1 (Titane) | 70 |
| 3 | 2 | -1 (300 µm) | +1 (100°) | -1 (Titane) | 56 |
| 4 | 6 | +1 (350 µm) | +1 (100°) | -1 (Titane) | 82 |
| 5 | 1 | -1 (300 µm) | -1 (50°) | 1 (Acier inoxydable) | 42 |
| 6 | 7 | +1 (350 µm) | -1 (50°) | 1 (Acier inoxydable) | 67 |
| 7 | 3 | -1 (300 µm) | +1 (100°) | 1 (Acier inoxydable) | 61 |
| 8 | 4 | +1 (350 µm) | +1 (100°) | 1 (Acier inoxydable) | 91 |
Le modèle matriciel correspondant est (où 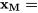 = coefficient de matériau) :
= coefficient de matériau) :
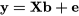

L’équation résultante est donc la suivante :