8.2.1 Variables catégoriques, variables indépendantes et variables muettes
- Une variable dichotomique, qui peut prendre les valeurs 0 ou 1.
- Une valeur de 1 représente la présence d’une qualité, un 0 son absence,
- Les 1 sont comparés aux 0, qui constituent le « groupe de référence ».
- Les variables muettes sont souvent considérées comme une approximation d’une variable qualitative.
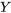 pour différents groupes nominaux dans les données. Ce type de test est similaire à un test d’écart moyen pour les groupes identifiés par la variable muette. Les variables muettes permettent de comparer un groupe inclus (les 1) et un groupe omis (les 0). Il est donc important d’indiquer clairement quel groupe est omis et sert de « catégorie de comparaison ».
pour différents groupes nominaux dans les données. Ce type de test est similaire à un test d’écart moyen pour les groupes identifiés par la variable muette. Les variables muettes permettent de comparer un groupe inclus (les 1) et un groupe omis (les 0). Il est donc important d’indiquer clairement quel groupe est omis et sert de « catégorie de comparaison ».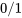 pour chaque catégorie, à l’exception du groupe de référence (qui est omis). Voici quelques exemples de variables catégoriques qui peuvent être représentées dans une régression multiple par des variables muettes :
pour chaque catégorie, à l’exception du groupe de référence (qui est omis). Voici quelques exemples de variables catégoriques qui peuvent être représentées dans une régression multiple par des variables muettes :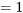 , contrôle
, contrôle 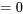 )
)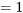 , femme
, femme 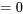 ou vice versa)
ou vice versa)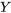 entre le groupe de la variable muette et le groupe de référence. Comme la différence estimée est la moyenne de toutes les observations
entre le groupe de la variable muette et le groupe de référence. Comme la différence estimée est la moyenne de toutes les observations 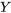 , il faut voir la variable muette comme un changement de la valeur de l’ordonnée à l’origine
, il faut voir la variable muette comme un changement de la valeur de l’ordonnée à l’origine 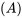 pour le groupe « muet », ce qui est illustré dans la figure 8.2.1.1. Dans ce graphique, la valeur de
pour le groupe « muet », ce qui est illustré dans la figure 8.2.1.1. Dans ce graphique, la valeur de 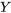 est fonction de
est fonction de 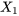 (une variable continue) et de
(une variable continue) et de 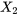 (une variable muette). Lorsque
(une variable muette). Lorsque 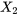 est égal à 0 (le cas de référence), c’est la droite de régression du haut qui s’applique. Lorsque
est égal à 0 (le cas de référence), c’est la droite de régression du haut qui s’applique. Lorsque 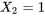 , la valeur de
, la valeur de 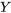 est réduite à la droite inférieure. En résumé, on peut estimer que
est réduite à la droite inférieure. En résumé, on peut estimer que 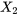 a un coefficient de régression partiel négatif, comme en témoigne la différence de hauteur entre les deux droites de régression.
a un coefficient de régression partiel négatif, comme en témoigne la différence de hauteur entre les deux droites de régression.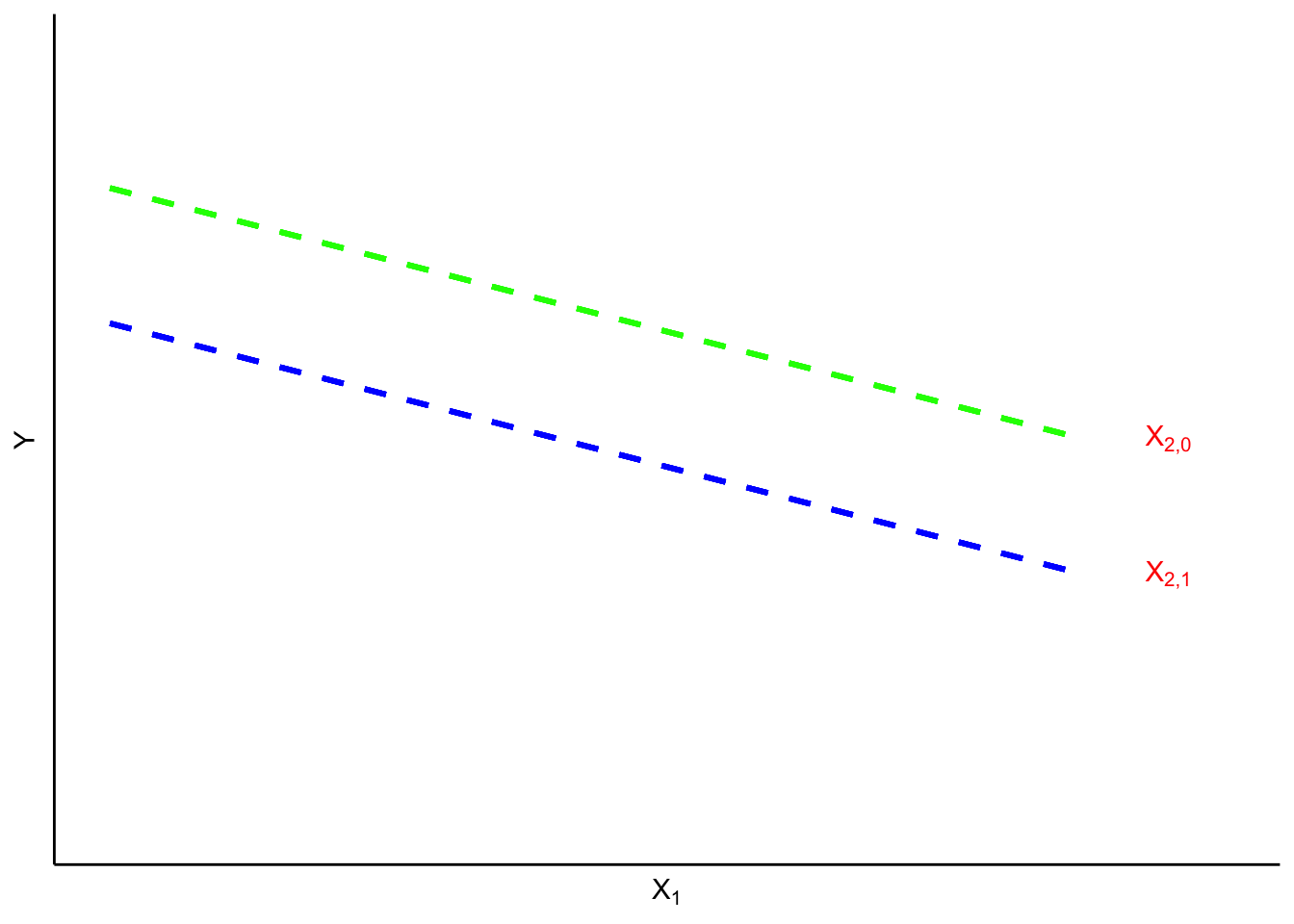
.
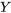 estimée entre les observations du Nord, de l’Est et de l’Ouest et celles du Sud.
estimée entre les observations du Nord, de l’Est et de l’Ouest et celles du Sud.Effets d’interaction et variables muettes
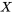 dépend de la valeur d’un autre. Typiquement, les modèles MCO sont additifs, c’est-à-dire qu’on additionne les
dépend de la valeur d’un autre. Typiquement, les modèles MCO sont additifs, c’est-à-dire qu’on additionne les 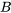 pour prédire
pour prédire 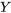 :
: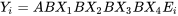 .
.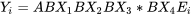 .
.Une « variable muette de pente » est un type particulier d’interaction dans lequel une variable muette a une interaction avec (est multipliée par) une variable d’échelle (ordinale ou supérieure). Supposons, par exemple, que l’on ait émis l’hypothèse que les effets de l’idéologie politique sur la perception des risques liés aux changements climatiques sont différents pour les hommes et pour les femmes. Les hommes sont peut-être plus susceptibles que les femmes d’intégrer systématiquement l’idéologie dans la perception des risques liés au changement climatique. Dans un tel cas, une variable muette 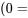 femmes,
femmes, 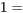 hommes
hommes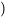 pourrait être associée à l’idéologie
pourrait être associée à l’idéologie 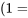 fortement à gauche,
fortement à gauche, 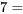 fortement à droite) pour prédire le niveau de risque perçu des changements climatiques (
fortement à droite) pour prédire le niveau de risque perçu des changements climatiques (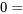 aucun risque,
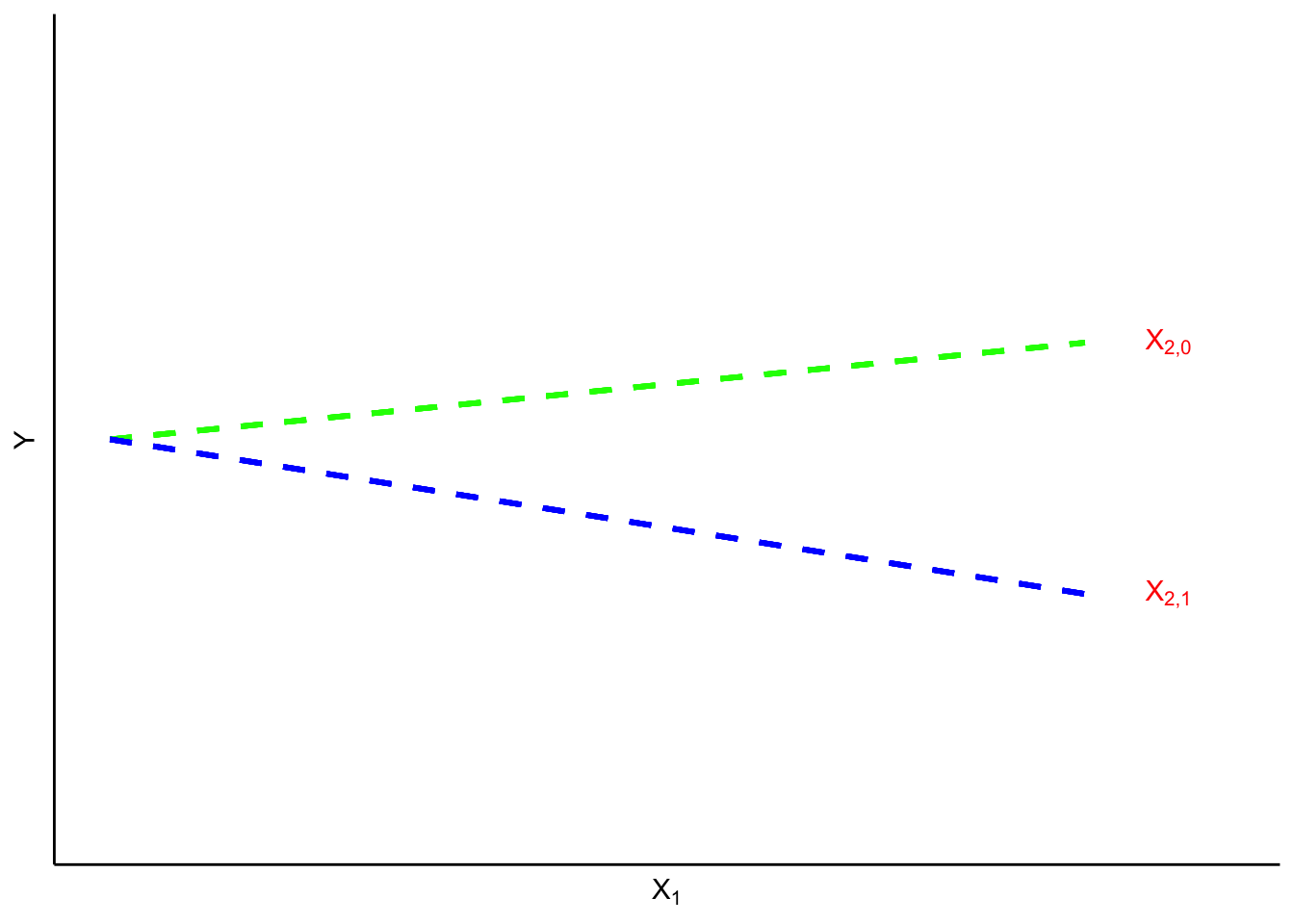
aucun risque, 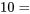 risque extrême). Si l’interaction hypothétique était correcte, on observerait une tendance comme celle illustrée à la figure 8.2.1.2.
risque extrême). Si l’interaction hypothétique était correcte, on observerait une tendance comme celle illustrée à la figure 8.2.1.2.
.
En somme, les variables muettes augmentent considérablement la flexibilité des modèles MCO. Elles permettent d’inclure des variables catégoriques et de tester des hypothèses sur les interactions entre les groupes et d’autres variables indépendantes au sein du modèle. Ce type de flexibilité est l’une des raisons pour lesquelles les modèles MCO sont largement utilisés dans le domaine des sciences sociales et de l’analyse politique.
Sources
Le contenu des chapitres 8.2.1.1 et 8.2.2.2 est issu de l’ouvrage Quantitative Research Methods for Political Science, Public Policy and Public Administration : 4th Edition With Applications in R, de Hank Jenkins-Smith, Joseph Ripberger, Gary Copeland, Matthew Nowlin, Tyler Hughes, Aaron Fister, Wesley Wehde, et Josie Davis, consultable à l’adresse https://bookdown.org/ripberjt/qrmbook/. Cet ouvrage est partagé sous licence Creative Commons Attribution 4.0 International (CC BY 4.0).
